Chào mừng các em học sinh đến với lời giải chi tiết bài tập 8 trang 81 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập 8 thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tính \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \) theo hằng số c dựa vào các vecto \(\mathop {SR}\limits^ \to ,\mathop {SQ}\limits^ \to ,\mathop {SP}\limits^ \to \). Sử dụng công thức \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = \mathop F\limits^ \to \) tìm c rồi thay ngược lại vào các vecto.
Đề bài
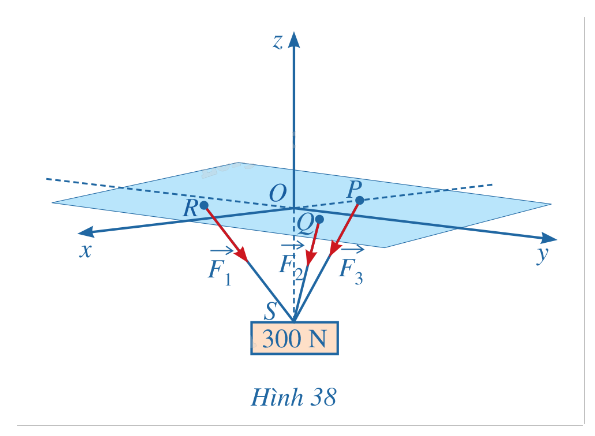
Một vật có trọng lượng 300N được treo bằng ba sợi dây cáp không dãn có chiều dài bằng nhau, mỗi dây cáp có một đầu được gắn tại một trog các điểm \(P( - 2;0;0),Q(1;\sqrt 3 ;0),R(1; - \sqrt 3 ;0)\) còn đầu kia gắn với vật tại điểm \(S(0;0; - 2\sqrt 3 )\) như Hình 28. Gọi \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \) lần lượt là lực căng trên các sợi dây cáp RS, QS và PS. Tìm tọa độ các lực \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \).\(\)
Phương pháp giải - Xem chi tiết
Tính \(\mathop {{F_1}}\limits^ \to ,\mathop {{F_2}}\limits^ \to ,\mathop {{F_3}}\limits^ \to \) theo hằng số c dựa vào các vecto \(\mathop {SR}\limits^ \to ,\mathop {SQ}\limits^ \to ,\mathop {SP}\limits^ \to \).
Sử dụng công thức \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = \mathop F\limits^ \to \) tìm c rồi thay ngược lại vào các vecto.
Lời giải chi tiết
Ta có: \(\mathop {SP}\limits^ \to = ( - 2;0;2\sqrt 3 ),\mathop {SQ}\limits^ \to = (1;\sqrt 3 ;2\sqrt 3 ),\mathop {SR}\limits^ \to = (1; - \sqrt 3 ;2\sqrt 3 )\).
Suy ra: \(\left| {\mathop {SP}\limits^ \to } \right| = \left| {\mathop {SQ}\limits^ \to } \right| = \left| {\mathop {SR}\limits^ \to } \right| = 4\).
Mặt khác: \(\mathop {SP}\limits^ \to = (3;\sqrt 3 ;0),\mathop {QR}\limits^ \to = (0; - 2\sqrt 3 ;0),\mathop {SR}\limits^ \to = ( - 3;\sqrt 3 ;0)\).
Suy ra: \(\left| {\mathop {QP}\limits^ \to } \right| = \left| {\mathop {QR}\limits^ \to } \right| = \left| {\mathop {RP}\limits^ \to } \right| = 2\sqrt 3 \) nên tam giác PQR đều.
Do đó: \(\left| {\mathop {{F_1}}\limits^ \to } \right| = \left| {\mathop {{F_2}}\limits^ \to } \right| = \left| {\mathop {{F_3}}\limits^ \to } \right|\). Tồn tại hằng số \(c \ne 0\) sao cho:
\(\mathop {{F_1}}\limits^ \to = c\mathop {SR}\limits^ \to = (c; - \sqrt 3 c;2\sqrt 3 c)\)
\(\mathop {{F_2}}\limits^ \to = c\mathop {SQ}\limits^ \to = (c;\sqrt 3 c;2\sqrt 3 c)\)
\(\mathop {{F_3}}\limits^ \to = c\mathop {SP}\limits^ \to = ( - 2c;0;2\sqrt 3 c)\)
Suy ra \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = (0;0;6\sqrt 3 c)\).
Mà \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = \mathop F\limits^ \to \), trong đó \(\mathop F\limits^ \to = (0;0; - 300)\) là trọng lực của vật.
Suy ra \(6\sqrt 3 c = - 300\), tức \(c = \frac{{ - 50\sqrt 3 }}{3}\).
Vậy \(\mathop {{F_1}}\limits^ \to = \left( {\frac{{ - 50\sqrt 3 }}{3};50; - 100} \right),\mathop {{F_2}}\limits^ \to = \left( {\frac{{ - 50\sqrt 3 }}{3}; - 50; - 100} \right);\mathop {{F_1}}\limits^ \to = \left( {\frac{{100\sqrt 3 }}{3};0; - 100} \right)\).
Bài tập 8 trang 81 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Bài tập 8 thường xoay quanh việc tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, tìm cực trị của hàm số và vẽ đồ thị hàm số. Cụ thể, bài tập có thể yêu cầu:
Để giải bài tập 8 trang 81 SGK Toán 12 tập 1 - Cánh diều, học sinh có thể áp dụng các bước sau:
Bài toán: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và vẽ đồ thị.
Giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | ĐB | NB |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập 8 trang 81 SGK Toán 12 tập 1 - Cánh diều một cách hiệu quả. Chúc các em học tập tốt!