Chào mừng bạn đến với bài học lý thuyết Phương trình đường thẳng Toán 12 Cánh Diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn một cách hệ thống và đầy đủ kiến thức về phương trình đường thẳng, bao gồm các khái niệm cơ bản, các dạng phương trình và ứng dụng của chúng.
Chúng tôi tin rằng, với sự hướng dẫn chi tiết và bài tập thực hành phong phú, bạn sẽ dễ dàng nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến phương trình đường thẳng trong kỳ thi Toán 12 sắp tới.
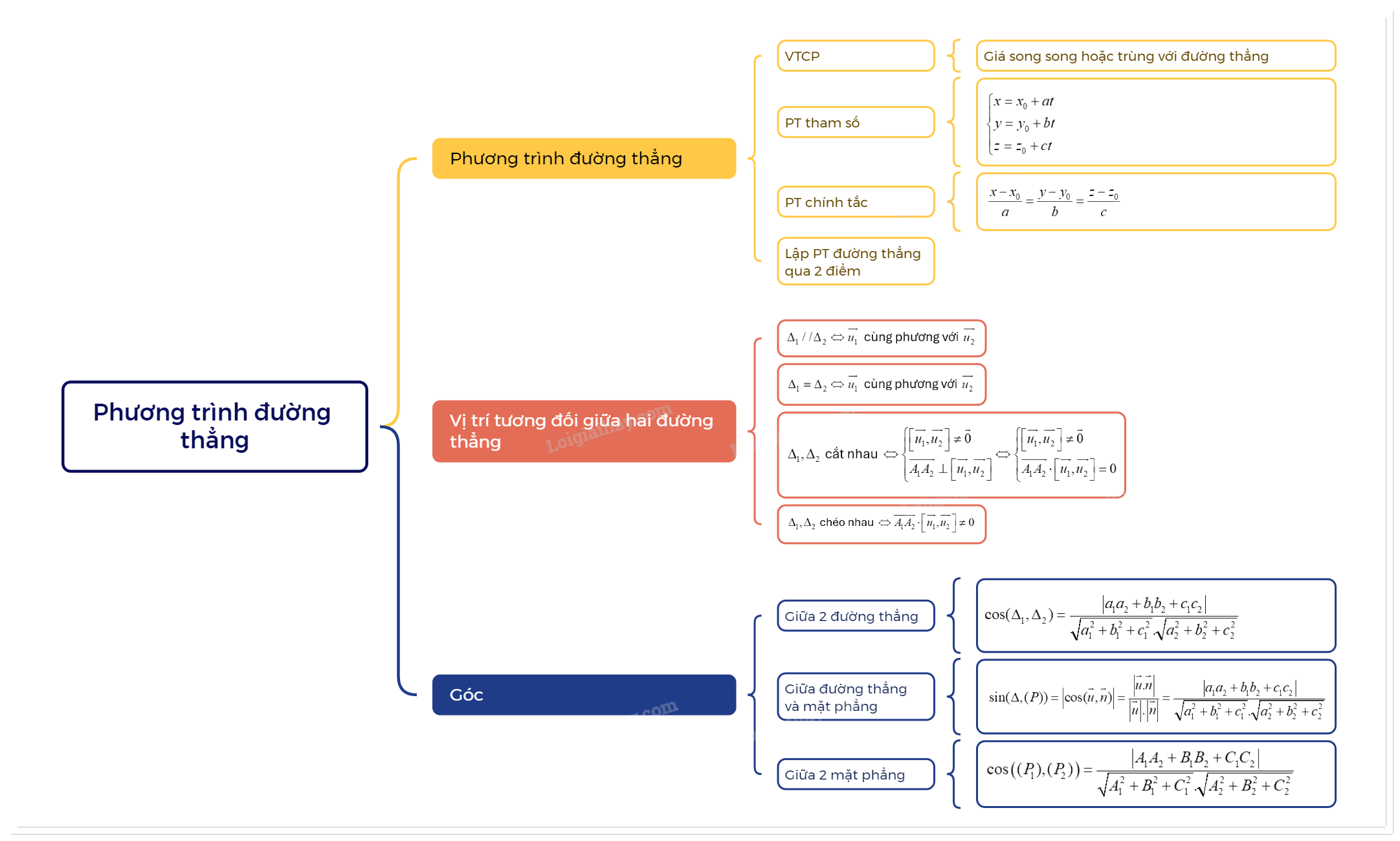
1. Phương trình đường thẳng a) Vecto chỉ phương của đường thẳng
1. Phương trình đường thẳng
a) Vecto chỉ phương của đường thẳng
| Vecto \(\overrightarrow u \ne \overrightarrow 0 \) được gọi là vecto chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \). |
b) Phương trình tham số của đường thẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\). Hệ phương trình: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) được gọi là phương trình tham số của đường thẳng \(\Delta \) (t là tham số, \(t \in R\)). |
c) Phương trình chính tắc của đường thẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) với a, b, c là các số khác 0. Hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \). |
d) Lập phương trình đường thẳng đi qua hai điểm
Trong không gian Oxyz, cho hai điểm phân biệt \({A_1}({x_1};{y_1};{z_1})\) và \({A_2}({x_2};{y_2};{z_2})\). Đường thẳng \({A_1}{A_2}\) có vecto chỉ phương \(\overrightarrow {{A_1}{A_2}} = ({x_2} - {x_1};{y_2} - {y_1};{z_2} - {z_1})\). - Đường thẳng \({A_1}{A_2}\) có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_1} + ({x_2} - {x_1})t\\y = {y_1} + ({y_2} - {y_1})t\\z = {z_1} + ({z_2} - {z_1})t\end{array} \right.\) \((t \in R)\). - Trong trường hợp \({x_1} \ne {x_2},{y_1} \ne {y_2},{z_1} \ne {z_2}\) thì đường thẳng \({A_1}{A_2}\) có phương trình chính tắc là: \(\frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{z - {z_1}}}{{{z_2} - {z_1}}}\). |
2. Vị trí tương đối giữa hai đường thẳng
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}({x_1};{y_1};{z_1})\), \({A_2}({x_2};{y_2};{z_2})\) và tương ứng có vecto chỉ phương \(\overrightarrow {{u_1}} ({x_1};{y_1};{z_1})\), \(\overrightarrow {{u_2}} ({x_2};{y_2};{z_2})\). Khi đó: + \({\Delta _1}//{\Delta _2} \Leftrightarrow \overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \notin {\Delta _2}\). + \({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\). + \({\Delta _1},{\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} \bot \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} \cdot \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\). + \({\Delta _1},{\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} \cdot \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\). |
3. Góc
a) Góc giữa hai đường thẳng
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) có vecto chỉ phương lần lượt là \(\overrightarrow {{u_1}} ({a_1};{b_1};{c_1})\), \(\overrightarrow {{u_2}} ({a_2};{b_2};{c_2})\). Khi đó, ta có: \(\cos ({\Delta _1},{\Delta _2}) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\) |
b) Góc giữa đường thẳng và mặt phẳng
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vecto chỉ phương lần lượt là \(\overrightarrow u ({a_1};{b_1};{c_1})\) và mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n ({a_2};{b_2};{c_2})\). Gọi \((\Delta ,(P))\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, ta có: \(\sin (\Delta ,(P)) = \left| {\cos (\overrightarrow u ,\overrightarrow n )} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\) |
c) Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng \(({P_1}),({P_2})\) là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó, kí hiệu là \(\left( {({P_1}),({P_2})} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(({P_1}),({P_2})\) có vecto pháp tuyến lần lượt là \(\overrightarrow {{n_1}} ({A_1};{B_1};{C_1})\), \(\overrightarrow {{n_2}} ({A_2};{B_2};{C_2})\). Khi đó, ta có: \(\cos \left( {({P_1}),({P_2})} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\) |
Phương trình đường thẳng là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 12, đặc biệt là trong chương trình Cánh Diều. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến phương trình đường thẳng là điều cần thiết để đạt kết quả tốt trong các kỳ thi.
Đường thẳng là tập hợp tất cả các điểm sao cho khoảng cách từ mỗi điểm đến một điểm cố định (gọi là điểm định hướng) và một đường thẳng cố định (gọi là đường thẳng định hướng) là không đổi. Phương trình đường thẳng là một phương trình biểu diễn tập hợp các điểm thuộc đường thẳng đó.
Có nhiều dạng phương trình đường thẳng khác nhau, mỗi dạng phù hợp với từng trường hợp cụ thể:
(x - x1) / (x2 - x1) = (y - y1) / (y2 - y1)
Vectơ chỉ phương của đường thẳng là một vectơ song song với đường thẳng đó. Nếu (a, b) là vectơ chỉ phương của đường thẳng ax + by + c = 0 thì đường thẳng đó cũng có vectơ chỉ phương là (b, -a).
Vectơ pháp tuyến của đường thẳng là một vectơ vuông góc với đường thẳng đó. Trong phương trình tổng quát ax + by + c = 0, (a, b) là vectơ pháp tuyến của đường thẳng.
Cho hai đường thẳng d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0:
Khoảng cách d từ điểm M(x0, y0) đến đường thẳng Δ: ax + by + c = 0 được tính theo công thức:
d = |ax0 + by0 + c| / √(a2 + b2)
Phương trình đường thẳng có nhiều ứng dụng trong thực tế, như:
Để củng cố kiến thức về phương trình đường thẳng, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Phương trình đường thẳng Toán 12 Cánh Diều. Chúc bạn học tập tốt!