Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2 - Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 12 trang 44, từ đó nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu, logic, kèm theo các ví dụ minh họa cụ thể để bạn có thể áp dụng vào các bài tập tương tự.
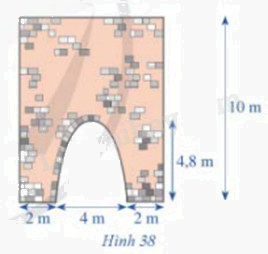
Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức tường đó. Chi phí để sơn lại bức tường là 15 000 đồng/ 1\({m^2}\). Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu
Đề bài
Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức tường đó. Chi phí để sơn lại bức tường là 15 000 đồng/ 1\({m^2}\). Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu
Phương pháp giải - Xem chi tiết
Tìm diện tích cánh cổng thông qua tích phân của hàm số biểu diễn cánh cổng đó trên hệ tọa độ. Từ đó tìm được diện tích cần sơn để tính chi phí
Lời giải chi tiết
Chọn hệ tọa độ Oxy có gốc tọa độ O(0;0) tại chân bên trái của bức tường
Cổng được biểu diễn trên hệ tọa độ bằng hàm số: \(y = a{x^2} + b\)
Đồ thị hàm số này đi qua điểm (2;0) và có đỉnh là (4;4,8), ta có: \(\left\{ \begin{array}{l}4a + b = 0\\16a + b = 4,8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0,4\\b = - 1,6\end{array} \right.\)
Vậy \(y = 0,4{x^2} - 1,6\)
Diện tích cánh cổng là: \(\int\limits_2^6 {\left( {0,4{x^2} - 1,6} \right)dx} = \left. {\left( {\frac{2}{{15}}{x^3} - 1,6x} \right)} \right|_2^6 = \frac{{64}}{3}{m^2}\)
Diện tích bức tường là: 10.8 = 80\({m^2}\)
Diện tích cần sơn là: \(80 - \frac{{64}}{3} = \frac{{176}}{3}{m^2}\)
Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó là: \(15000.\frac{{176}}{3} = 880000\)(đồng)
Bài tập 12 trang 44 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp để giải quyết các bài toán cụ thể. Việc nắm vững các quy tắc đạo hàm và kỹ năng biến đổi đại số là rất quan trọng để giải quyết bài tập này một cách hiệu quả.
Bài tập 12 thường bao gồm các dạng bài sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lưu ý rằng, trong quá trình giải bài, bạn cần:
Câu a: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Đạo hàm là một khái niệm quan trọng trong toán học, có nhiều ứng dụng trong các lĩnh vực khác nhau như vật lý, kinh tế, và kỹ thuật. Việc hiểu rõ về đạo hàm sẽ giúp bạn giải quyết các bài toán phức tạp hơn và có cái nhìn sâu sắc hơn về thế giới xung quanh.
Hy vọng rằng, với lời giải chi tiết và các lưu ý quan trọng được trình bày trong bài viết này, bạn đã có thể tự tin giải quyết bài tập 12 trang 44 SGK Toán 12 tập 2 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!