Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 5, 6, 7 sách giáo khoa Toán 12 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 12 Cánh diều
a) Xác định tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^3}\).
b) Xét dấu của đạo hàm \(f'\left( x \right) = 3{x^2}\).
c) Phương trình \(f'\left( x \right) = 0\) có bao nhiêu nghiệm ?
Phương pháp giải:
Dựa vào định nghĩa đồng biến, nghịch biến của hàm số và các bước xét tính đồng biến, nghịch biến của hàm số
Lời giải chi tiết:
a) Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2}\).
Xét \(y' = 0 \Rightarrow x = 0\).
Bảng biến thiên:
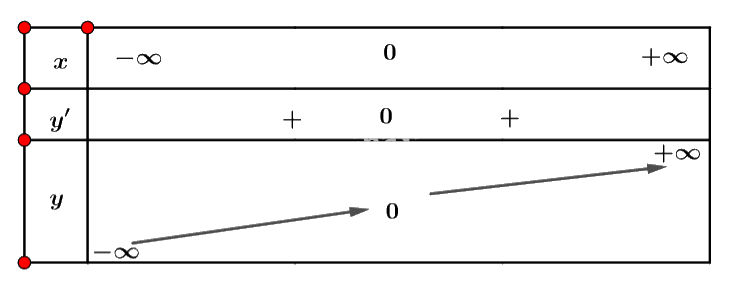
Vậy hàm số đồng biến trên \(\mathbb{R}\).
b) Dựa vào bảng biến thiên ta thấy đạo hàm \(y' = 3{x^2}\) luôn dương với mọi x.
c) Phương trình \(f'\left( x \right) = 0\) có một nghiệm.
Trả lời câu hỏi Hoạt động 1 trang 5 SGK Toán 12 Cánh diều
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
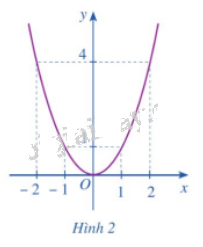
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Xét dấu đạo hàm \(f'\left( x \right) = 2x\).
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f'\left( x \right) = 2x\) trên mỗi khoảng \(\left( { - \infty ;0} \right),\left( {0; + \infty } \right)\).
- Hoàn thành bảng biến thiên sau:
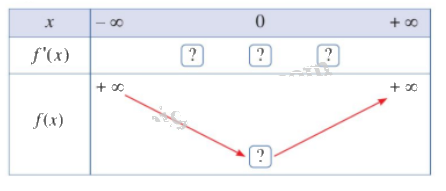
Phương pháp giải:
Dựa vào định nghĩa hàm số đồng biến, nghịch biến trên tập K
Lời giải chi tiết:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và \(f\left( x \right)\) là hàm số xác định trên K.
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
- Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
- Đạo hàm \(f'\left( x \right) = 2x\)âm khi \(x < 0\) và dương khi \(x > 0\).
- Hàm số \(y = f\left( x \right) = {x^2}\) nghịch biến khi \(f'\left( x \right) = 2x\)mang dấu âm và đồng biến khi \(f'\left( x \right) = 2x\) mang dấu dương.
- Ta có bàng biến thiên sau:
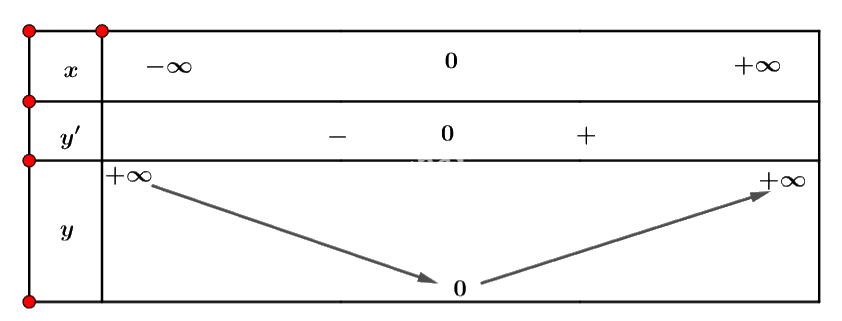
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số \(y = {x^4} + 2{x^2} - 3\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} + 4x\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
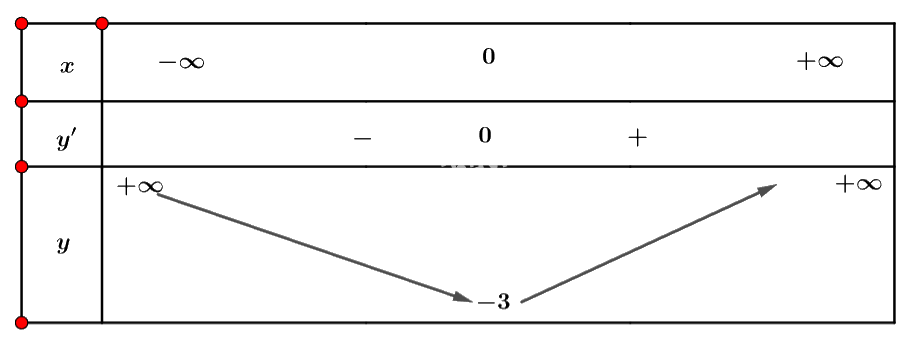
Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Trả lời câu hỏi Luyện tập 3 trang 7 SGK Toán 12 Cánh diều
Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }}\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
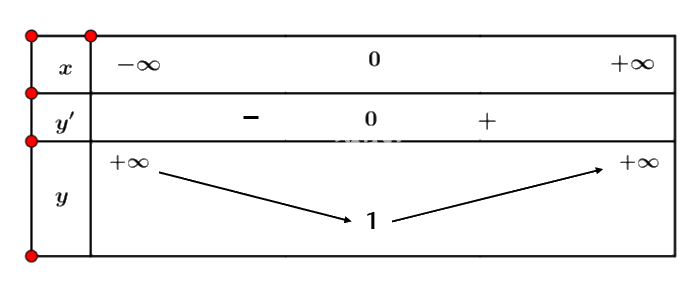
Vậy hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Trả lời câu hỏi Luyện tập 4 trang 8 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số sau \(y = \frac{{2x - 1}}{{x + 2}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}}\).
Nhận xét: \(y' > 0\) với mọi \(x \in D\).
Ta có bảng biến thiên:
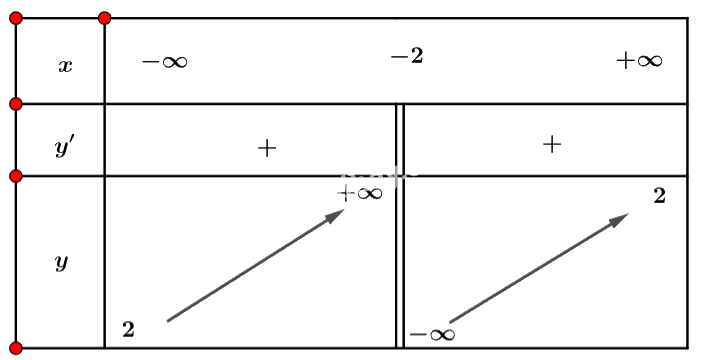
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Cánh diều
Xét dấu \(y'\) rồi tìm khoảng đồng biến, nghịch biến của hàm số\(y = \frac{4}{3}{x^3} - 2{x^2} + x - 1\).
Phương pháp giải:
B1: Tính \(y'\)rồi lập bảng xét dấu của \(y'\).
B2. Dựa vào bảng xét dấu của \(y'\) để nhận xét khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^2} - 4x + 1\).
Xét \(y' = 0 \Leftrightarrow x = \frac{1}{2}\).

Vậy hàm số đồng biến trên \(\mathbb{R}\).
Trả lời câu hỏi Hoạt động 1 trang 5 SGK Toán 12 Cánh diều
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
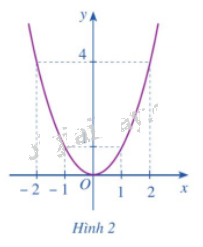
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Xét dấu đạo hàm \(f'\left( x \right) = 2x\).
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f'\left( x \right) = 2x\) trên mỗi khoảng \(\left( { - \infty ;0} \right),\left( {0; + \infty } \right)\).
- Hoàn thành bảng biến thiên sau:
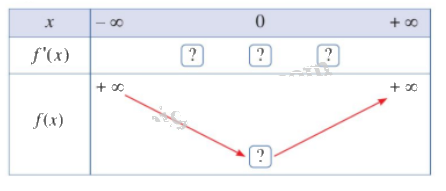
Phương pháp giải:
Dựa vào định nghĩa hàm số đồng biến, nghịch biến trên tập K
Lời giải chi tiết:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và \(f\left( x \right)\) là hàm số xác định trên K.
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
- Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
- Đạo hàm \(f'\left( x \right) = 2x\)âm khi \(x < 0\) và dương khi \(x > 0\).
- Hàm số \(y = f\left( x \right) = {x^2}\) nghịch biến khi \(f'\left( x \right) = 2x\)mang dấu âm và đồng biến khi \(f'\left( x \right) = 2x\) mang dấu dương.
- Ta có bàng biến thiên sau:
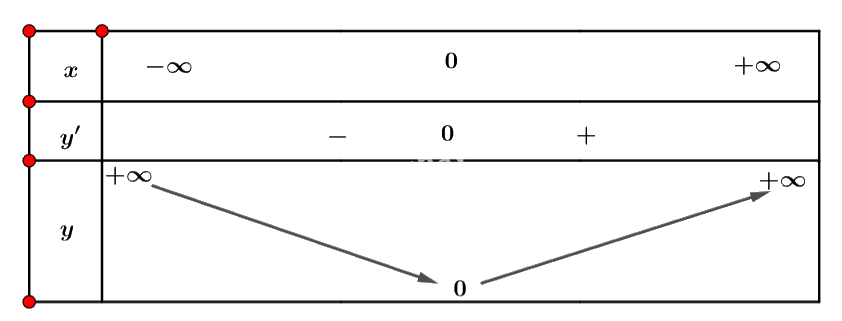
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Cánh diều
Xét dấu \(y'\) rồi tìm khoảng đồng biến, nghịch biến của hàm số\(y = \frac{4}{3}{x^3} - 2{x^2} + x - 1\).
Phương pháp giải:
B1: Tính \(y'\)rồi lập bảng xét dấu của \(y'\).
B2. Dựa vào bảng xét dấu của \(y'\) để nhận xét khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^2} - 4x + 1\).
Xét \(y' = 0 \Leftrightarrow x = \frac{1}{2}\).

Vậy hàm số đồng biến trên \(\mathbb{R}\).
Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số \(y = {x^4} + 2{x^2} - 3\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} + 4x\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
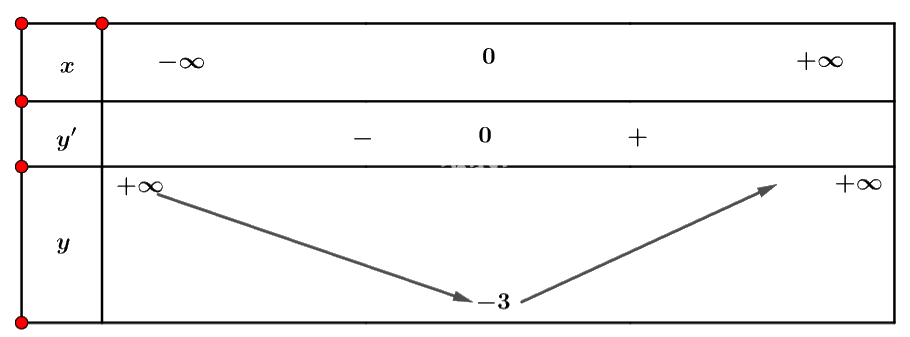
Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 12 Cánh diều
a) Xác định tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^3}\).
b) Xét dấu của đạo hàm \(f'\left( x \right) = 3{x^2}\).
c) Phương trình \(f'\left( x \right) = 0\) có bao nhiêu nghiệm ?
Phương pháp giải:
Dựa vào định nghĩa đồng biến, nghịch biến của hàm số và các bước xét tính đồng biến, nghịch biến của hàm số
Lời giải chi tiết:
a) Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2}\).
Xét \(y' = 0 \Rightarrow x = 0\).
Bảng biến thiên:
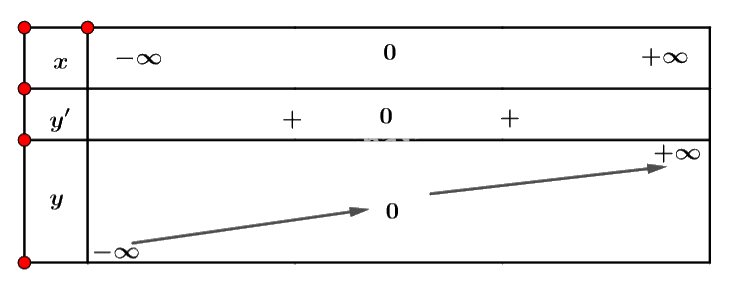
Vậy hàm số đồng biến trên \(\mathbb{R}\).
b) Dựa vào bảng biến thiên ta thấy đạo hàm \(y' = 3{x^2}\) luôn dương với mọi x.
c) Phương trình \(f'\left( x \right) = 0\) có một nghiệm.
Trả lời câu hỏi Luyện tập 3 trang 7 SGK Toán 12 Cánh diều
Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }}\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:
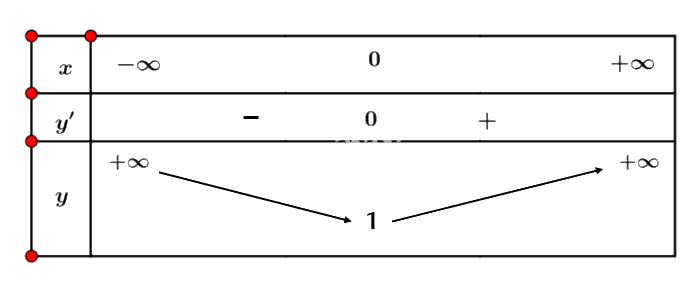
Vậy hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Trả lời câu hỏi Luyện tập 4 trang 8 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số sau \(y = \frac{{2x - 1}}{{x + 2}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}}\).
Nhận xét: \(y' > 0\) với mọi \(x \in D\).
Ta có bảng biến thiên:
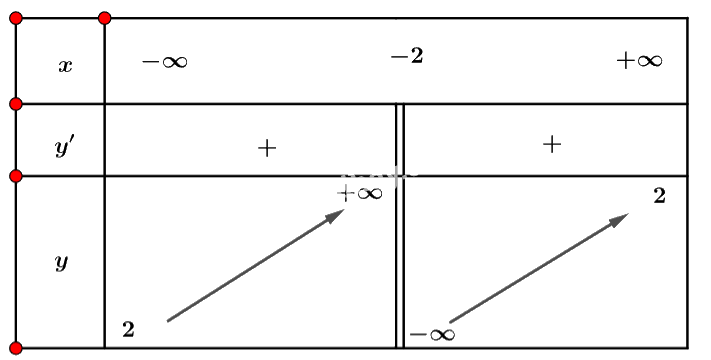
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Mục 1 của chương trình Toán 12 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số và đồ thị. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong các chương tiếp theo. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và vẽ đồ thị hàm số.
Bài 1 yêu cầu học sinh xác định tập xác định của hàm số. Để giải bài này, học sinh cần nắm vững điều kiện xác định của các loại hàm số khác nhau, như hàm số phân thức, hàm số căn thức, hàm số logarit. Ví dụ, với hàm số y = 1/(x-2), tập xác định là R \ {2}.
Bài 2 tập trung vào việc tìm giao điểm của đồ thị hàm số và đường thẳng. Để giải bài này, học sinh cần giải phương trình hoành độ giao điểm, tức là giải phương trình f(x) = g(x), trong đó f(x) là hàm số và g(x) là phương trình đường thẳng. Sau khi tìm được nghiệm của phương trình, học sinh thay nghiệm đó vào phương trình đường thẳng để tìm tung độ giao điểm.
Bài 3 yêu cầu học sinh xét tính đơn điệu của hàm số. Để giải bài này, học sinh có thể sử dụng phương pháp xét dấu đạo hàm. Nếu đạo hàm f'(x) > 0 trên một khoảng, hàm số f(x) đồng biến trên khoảng đó. Nếu đạo hàm f'(x) < 0 trên một khoảng, hàm số f(x) nghịch biến trên khoảng đó.
Ví dụ: Giải phương trình 2x = 8.
Lời giải: Ta có 2x = 23, suy ra x = 3.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh nên làm thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Ngoài ra, học sinh có thể tham khảo các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 12 tập 1 - Cánh diều. Chúc các em học tốt!