Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Cánh diều. Bài tập 13 trang 48 thuộc chương trình học quan trọng, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi cam kết mang đến cho bạn những giải pháp tối ưu, giúp bạn hiểu sâu sắc nội dung bài học và tự tin hơn trong các kỳ thi.
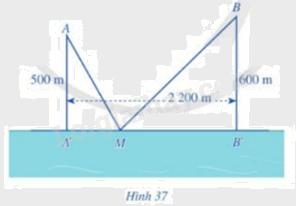
Có hai xã A,B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ =500m, BB’=600m và người ta đo được A’B’= 2.200m(hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xa đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Đề bài
Có hai xã A,B cùng ở một bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA’ =500m, BB’=600m và người ta đo được A’B’= 2.200m(hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A’B’ sao cho tổng khoảng cách từ hai xa đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Phương pháp giải - Xem chi tiết
- Phân tích đề bài
- Tìm mối liên hệ trong bài
Lời giải chi tiết
Đặt A'M = x (m).
Suy ra B'M = A'B' – A'M = 2200 – x (m).
Rõ ràng, x phải thỏa mãn điều kiện 0 < x < 2200.
Áp dụng định lí Pythagore ta tính được:
\(AM = \sqrt {A'{A^2} + A'{M^2}} {\rm{\;}} = \sqrt {{{500}^2} + {x^2}} \) (m)
\(BM = \sqrt {B'{B^2} + B'{M^2}} {\rm{\;}} = \sqrt {{{600}^2} + {{(2200 - x)}^2}} \) (m)
Tổng khoảng cách từ hai vị trí A, B đến vị trí M là
\(D = AM + BM = \sqrt {{{500}^2} + {x^2}} {\rm{\;}} + \sqrt {{{600}^2} + {{(2200 - x)}^2}} \) (m)
Xét hàm số \(D(x) = \sqrt {{{500}^2} + {x^2}} {\rm{\;}} + \sqrt {{{600}^2} + (2200 - {x^2})} \) với \(x \in (0;2200)\).
\(D'(x) = \frac{{2x}}{{2\sqrt {{{500}^2} + {x^2}} }} + \frac{{2x - 4400}}{{\sqrt {{{600}^2} + {{(2200 - x)}^2}} }} = \frac{x}{{\sqrt {{{500}^2} + {x^2}} }} + \frac{{x - 2200}}{{\sqrt {{{600}^2} + {{(2200 - x)}^2}} }}\).
Trên khoảng (0;2200), ta thấy D'(x) = 0 khi x = 1000.
Bảng biến thiên của hàm số D(x) như sau:
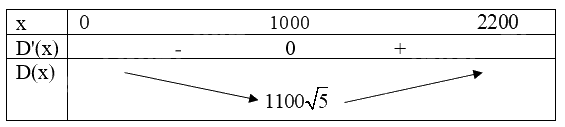
Căn cứ vào bảng biến thiên, ta thấy hàm số D(x) đạt giá trị nhỏ nhất bằng \(1100\sqrt 5 \) tại x = 1 000.
Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là \(1100\sqrt 5 \) m.
Bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc tính đạo hàm của hàm số, xét tính đơn điệu của hàm số và tìm cực trị. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các công thức đạo hàm cơ bản, các quy tắc tính đạo hàm và các phương pháp xét tính đơn điệu của hàm số.
Bài tập 13 thường bao gồm các câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều, học sinh có thể áp dụng các phương pháp sau:
Bài toán: Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.
Giải:
f'(x) = 3x2 - 6x + 2
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 12 tập 1 - Cánh diều và các tài liệu tham khảo khác.
Việc giải bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều không chỉ giúp học sinh nắm vững kiến thức về đạo hàm mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong nhiều lĩnh vực khác của cuộc sống.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các bạn học sinh đã có thể tự tin giải quyết bài tập 13 trang 48 SGK Toán 12 tập 1 - Cánh diều. Chúc các bạn học tập tốt và đạt kết quả cao trong môn Toán!