Giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 2 - Cánh diều. Bài viết này sẽ giúp bạn giải quyết triệt để bài tập 11 trang 64, nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả cao trong môn Toán.

Hình 20 minh họa hình ảnh một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là mét). Biết A(50;0;0), D(0;20;0), B(4k;3k;2k) với k > 0 và mặt phẳng (CBEF) có phương trình z = 3 a) Tìm tọa độ điểm B b) Lập phương trình mặt phẳng (AOBC) c) Lập phương trình mặt phẳng (DOBE) d) Chỉ ra một vecto pháp tuyến của mỗi mặt phẳng (AOBC) và (DOBE)

Đề bài

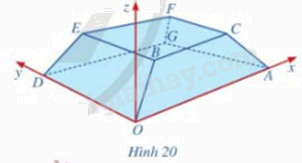
Giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều 1

a) Tìm tọa độ điểm B.

b) Lập phương trình mặt phẳng (AOBC).

c) Lập phương trình mặt phẳng (DOBE).

d) Chỉ ra một vecto pháp tuyến của mỗi mặt phẳng (AOBC) và (DOBE).

Phương pháp giải - Xem chi tiết Giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều 2

a) Thay tọa độ điểm B vào phương trình mặt phẳng (CBEF).

b), c) Tìm cặp vecto chỉ phương của mặt phẳng để tìm vecto pháp tuyến. Sử dụng phương trình tổng quát của mặt phẳng.

d) Sử dụng kết quả phần b) và c).

Lời giải chi tiết

a) Ta có \(B \in (CBEF):2k = 3 \Leftrightarrow k = \frac{3}{2}\).

Vậy \(B(6;\frac{9}{2};3)\).

b) \(\overrightarrow {OA} = (50;0;0);\overrightarrow {OB} = (6;\frac{9}{2};3)\).

Vecto pháp tuyến của mặt phẳng (AOBC) là: \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = (0; - 150;225) = 75(0; - 2;3)\).

Phương trình mặt phẳng (AOB) là: -2y + 3z = 0.

Vậy phương trình mặt phẳng (AOBC) là -2y + 3z = 0.

c) \(\overrightarrow {OD} = (0;20;0)\).

Vecto pháp tuyến của mặt phẳng (AOBC) là: \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {OD} ;\overrightarrow {OB} } \right] = (60;0; - 120) = 60(1;0; - 2)\).

Phương trình mặt phẳng (DOB) là: x - 2z = 0.

Vậy phương trình mặt phẳng (DOBE) là x - 2z = 0.

d) Vecto pháp tuyến của mặt phẳng (AOBC) và (DOBE) lần lượt là \(\overrightarrow {{n_1}} = (0; - 2;3)\) và \(\overrightarrow {{n_2}} = (1;0; - 2)\).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều đặc sắc thuộc chuyên mục bài tập toán 12 trên nền tảng toán math. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều: Tổng quan

Bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về Đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tính đạo hàm, tìm cực trị, và khảo sát hàm số. Việc nắm vững các công thức đạo hàm cơ bản và các quy tắc tính đạo hàm là vô cùng quan trọng để giải quyết bài tập này một cách hiệu quả.

Nội dung bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều

Bài tập 11 thường có dạng như sau: Cho hàm số y = f(x). Tính đạo hàm f'(x) và xác định các điểm cực trị của hàm số. Hoặc, bài tập có thể yêu cầu học sinh sử dụng đạo hàm để giải các bài toán thực tế liên quan đến tối ưu hóa.

Phương pháp giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều

Bước 1: Tính đạo hàm f'(x): Sử dụng các công thức đạo hàm cơ bản và quy tắc tính đạo hàm (quy tắc tổng, hiệu, tích, thương, hàm hợp) để tính đạo hàm của hàm số f(x).
Bước 2: Tìm các điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghiệm. Các điểm nghiệm này là các điểm cực trị của hàm số.
Bước 3: Xác định loại cực trị: Sử dụng dấu của đạo hàm cấp hai f''(x) hoặc xét dấu của f'(x) xung quanh các điểm nghiệm để xác định loại cực trị (cực đại hoặc cực tiểu).
Bước 4: Kết luận: Viết kết luận về các điểm cực trị của hàm số.

Ví dụ minh họa giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều

Ví dụ: Cho hàm số y = x³ - 3x² + 2. Tìm các điểm cực trị của hàm số.

Giải:

Bước 1: Tính đạo hàm: y' = 3x² - 6x
Bước 2: Tìm các điểm cực trị: Giải phương trình y' = 0, ta được 3x² - 6x = 0 => x = 0 hoặc x = 2
Bước 3: Xác định loại cực trị: y'' = 6x - 6. Tại x = 0, y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0. Tại x = 2, y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2.
Bước 4: Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Lưu ý khi giải bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều

Nắm vững các công thức đạo hàm cơ bản và quy tắc tính đạo hàm.
Kiểm tra kỹ các bước tính toán để tránh sai sót.
Sử dụng đạo hàm cấp hai hoặc xét dấu của đạo hàm cấp một để xác định chính xác loại cực trị.
Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.

Các bài tập tương tự và tài liệu tham khảo

Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 2 - Cánh diều và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi THPT Quốc gia để được hướng dẫn chi tiết và giải đáp thắc mắc.

Kết luận

Bài tập 11 trang 64 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán.