Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 17, 18, 19 sách giáo khoa Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Định nghĩa tích phân
Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Cánh diều
Cho hàm số \(f(x) = {x^2}\)
a) Chứng tỏ \(F(x) = \frac{{{x^3}}}{3}\), \(G(x) = \frac{{{x^3}}}{3} + C\) là các nguyên hàm của hàm số \(f(x) = {x^2}\)
b) Chứng minh rằng \(F(b) - F(a) = G(b) - G(a)\), tức là hiệu số \(F(b) - F(a)\) không phụ thuộc việc chọn nguyên hàm
Phương pháp giải:
Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K
Lời giải chi tiết:
a) \(F'(x) = G'(x) = {x^2} = f(x)\) nên \(F(x) = \frac{{{x^3}}}{3}\), \(G(x) = \frac{{{x^3}}}{3} + C\) là các nguyên hàm của hàm số \(f(x) = {x^2}\)
b) \(F(b) - F(a) = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}\)
\(G(b) - G(a) = \frac{{{b^3}}}{3} + C - \frac{{{a^3}}}{3} - C = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}\)
=> \(F(b) - F(a) = G(b) - G(a)\)
Trả lời câu hỏi Hoạt động 1 trang 17 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^2}\) (Hình 4). Xét hình phẳng (được tô màu) gồm tất cả điểm M(x;y) trên mặt phẳng tọa độ sao cho \(1 \le x \le 2\) và \(0 \le y \le {x^2}\). Hình phẳng đó được gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số \(f(x) = {x^2}\), trục Ox và hai đường thẳng x = 1 và x = 2
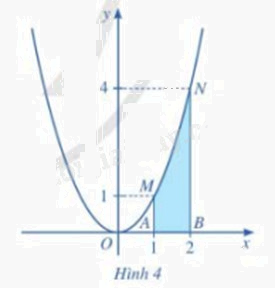
Chia đoạn [1;2] thành n phần bằng nhau bởi các điểm chia: \({x_0} = 1,{x_1} = 1 + \frac{1}{n},{x_2} = 1 + \frac{2}{n},...,{x_{n - 1}} = 1 + \frac{{n - 1}}{n},{x_n} = 1 + \frac{n}{n} = 2\) (Hình 5)
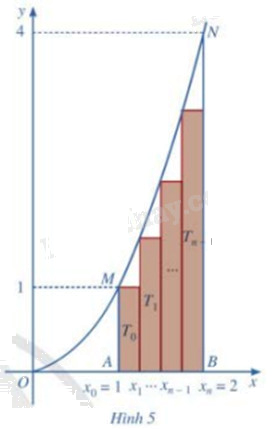
a) Tính diện tích \({T_0}\) của hình chữ nhật dựng trên đoạn \([{x_0};{x_1}]\) với chiều cao là \(f({x_0})\)
Tính diện tích \({T_1}\) của hình chữ nhật dựng trên đoạn \([{x_1};{x_2}]\) với chiều cao là \(f({x_1})\)
Tính diện tích \({T_2}\) của hình chữ nhật dựng trên đoạn \([{x_2};{x_3}]\) với chiều cao là \(f({x_2})\)
…
Tính diện tích \({T_{n - 1}}\) của hình chữ nhật dựng trên đoạn \([{x_{n - 1}};{x_n}]\) với chiều cao là \(f({x_{n - 1}})\)
b) Đặt \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}}\). Chứng minh rằng: \({S_n} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\). Tổng \({S_n}\) gọi là tổng tích phân cấp n của hàm số \(f(x) = {x^2}\) trên đoạn [1;2]
Phương pháp giải:
a) Áp dụng công thức tính diện tích hình chữ nhật
b) Biến đổi biểu thức cho thích hợp
Lời giải chi tiết:
a) \({T_0} = f({x_0}).({x_1} - {x_0}) = f(1).({x_1} - 1)\)
\({T_1} = f({x_1}).({x_2} - {x_1})\)
\({T_2} = f({x_2}).({x_3} - {x_2})\)
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})\) b) \({T_0} = f({x_0}).({x_1} - {x_0}) = f({x_0}).({x_0} + \frac{1}{n} - {x_0}) = \frac{{f({x_0})}}{n}\)
\({T_1} = f({x_1}).({x_2} - {x_1}) = f({x_1}).({x_1} + \frac{1}{n} - {x_1}) = \frac{{f({x_1})}}{n}\)
\({T_2} = f({x_2}).({x_3} - {x_2}) = f({x_2}).({x_2} + \frac{1}{n} - {x_2}) = \frac{{f({x_2})}}{n}\)
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}}) = f({x_{n - 1}}).({x_{n - 1}} + \frac{1}{n} - {x_{n - 1}}) = \frac{{f({x_{n - 1}})}}{n}\)
Vậy \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\)
Trả lời câu hỏi Hoạt động 1 trang 17 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^2}\) (Hình 4). Xét hình phẳng (được tô màu) gồm tất cả điểm M(x;y) trên mặt phẳng tọa độ sao cho \(1 \le x \le 2\) và \(0 \le y \le {x^2}\). Hình phẳng đó được gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số \(f(x) = {x^2}\), trục Ox và hai đường thẳng x = 1 và x = 2
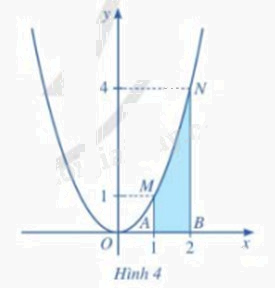
Chia đoạn [1;2] thành n phần bằng nhau bởi các điểm chia: \({x_0} = 1,{x_1} = 1 + \frac{1}{n},{x_2} = 1 + \frac{2}{n},...,{x_{n - 1}} = 1 + \frac{{n - 1}}{n},{x_n} = 1 + \frac{n}{n} = 2\) (Hình 5)
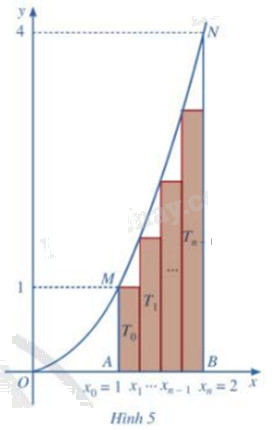
a) Tính diện tích \({T_0}\) của hình chữ nhật dựng trên đoạn \([{x_0};{x_1}]\) với chiều cao là \(f({x_0})\)
Tính diện tích \({T_1}\) của hình chữ nhật dựng trên đoạn \([{x_1};{x_2}]\) với chiều cao là \(f({x_1})\)
Tính diện tích \({T_2}\) của hình chữ nhật dựng trên đoạn \([{x_2};{x_3}]\) với chiều cao là \(f({x_2})\)
…
Tính diện tích \({T_{n - 1}}\) của hình chữ nhật dựng trên đoạn \([{x_{n - 1}};{x_n}]\) với chiều cao là \(f({x_{n - 1}})\)
b) Đặt \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}}\). Chứng minh rằng: \({S_n} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\). Tổng \({S_n}\) gọi là tổng tích phân cấp n của hàm số \(f(x) = {x^2}\) trên đoạn [1;2]
Phương pháp giải:
a) Áp dụng công thức tính diện tích hình chữ nhật
b) Biến đổi biểu thức cho thích hợp
Lời giải chi tiết:
a) \({T_0} = f({x_0}).({x_1} - {x_0}) = f(1).({x_1} - 1)\)
\({T_1} = f({x_1}).({x_2} - {x_1})\)
\({T_2} = f({x_2}).({x_3} - {x_2})\)
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})\) b) \({T_0} = f({x_0}).({x_1} - {x_0}) = f({x_0}).({x_0} + \frac{1}{n} - {x_0}) = \frac{{f({x_0})}}{n}\)
\({T_1} = f({x_1}).({x_2} - {x_1}) = f({x_1}).({x_1} + \frac{1}{n} - {x_1}) = \frac{{f({x_1})}}{n}\)
\({T_2} = f({x_2}).({x_3} - {x_2}) = f({x_2}).({x_2} + \frac{1}{n} - {x_2}) = \frac{{f({x_2})}}{n}\)
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}}) = f({x_{n - 1}}).({x_{n - 1}} + \frac{1}{n} - {x_{n - 1}}) = \frac{{f({x_{n - 1}})}}{n}\)
Vậy \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\)
Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Cánh diều
Cho hàm số \(f(x) = {x^2}\)
a) Chứng tỏ \(F(x) = \frac{{{x^3}}}{3}\), \(G(x) = \frac{{{x^3}}}{3} + C\) là các nguyên hàm của hàm số \(f(x) = {x^2}\)
b) Chứng minh rằng \(F(b) - F(a) = G(b) - G(a)\), tức là hiệu số \(F(b) - F(a)\) không phụ thuộc việc chọn nguyên hàm
Phương pháp giải:
Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K
Lời giải chi tiết:
a) \(F'(x) = G'(x) = {x^2} = f(x)\) nên \(F(x) = \frac{{{x^3}}}{3}\), \(G(x) = \frac{{{x^3}}}{3} + C\) là các nguyên hàm của hàm số \(f(x) = {x^2}\)
b) \(F(b) - F(a) = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}\)
\(G(b) - G(a) = \frac{{{b^3}}}{3} + C - \frac{{{a^3}}}{3} - C = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}\)
=> \(F(b) - F(a) = G(b) - G(a)\)
Mục 1 của chương trình Toán 12 tập 2 - Cánh diều tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng, nền tảng cho việc giải quyết nhiều bài toán trong các chương tiếp theo. Việc nắm vững các khái niệm, định lý và kỹ năng tính đạo hàm là điều cần thiết để đạt kết quả cao trong môn Toán.
Bài tập này yêu cầu học sinh vận dụng các quy tắc tính đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp. Cần chú ý đến việc xác định đúng các hàm số thành phần và áp dụng quy tắc một cách chính xác.
Bài tập này yêu cầu học sinh sử dụng định nghĩa đạo hàm để tính đạo hàm của hàm số tại một điểm cụ thể. Cần lưu ý đến việc tính toán giới hạn một cách chính xác.
Định nghĩa: Đạo hàm của hàm số y = f(x) tại x = x0 được định nghĩa là: f'(x0) = limh→0 [f(x0 + h) - f(x0)] / h
Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến vận tốc, gia tốc, tối ưu hóa và các bài toán thực tế khác. Cần phân tích bài toán một cách kỹ lưỡng để xác định đúng các đại lượng cần tìm và áp dụng đạo hàm một cách phù hợp.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 17,18,19 SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!