Chào mừng các em học sinh đến với lời giải chi tiết bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 14 thuộc chương trình học Toán 12 tập 2, tập trung vào các kiến thức về...
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là (overrightarrow u = left( {91;75;0} right)) hướng về đài kiểm soát không lưu (Hình 44).
Đề bài
Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {91;75;0} \right)\) hướng về đài kiểm soát không lưu (Hình 44).
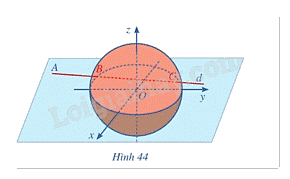
a) Xác định toạ độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
b) Xác định toạ độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.
c) Xác định toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa.
Phương pháp giải - Xem chi tiết
a) + Viết phương trình đường thẳng d đi qua điểm A và có một vectơ chỉ phương \(\overrightarrow u \).
+ Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa. B thuộc d nên tính tọa độ của B theo t.
+ B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì \(OB = 417\). Từ đó có phương trình theo ẩn t, giải phương trình tính t.
+ Thay giá trị t tính được để tìm tọa độ B, so sánh giá trị và được ra kết luận.
b) + Gọi H là vị trí mà máy bay gần đài kiểm soát không lưu nhất.
+ Vì H thuộc d nên tính tọa độ của H theo t’.
+ OH ngắn nhất khi và chỉ khi \(OH \bot d \Leftrightarrow \overrightarrow {OH} \bot \overrightarrow u \Leftrightarrow \overrightarrow {OH} .\overrightarrow u = 0\), từ đó tính được t’.
+ Từ đó tính được H và khoảng cách OH cần tìm.
Lời giải chi tiết
a) Đường thẳng d đi qua điểm A(-688;-185;8), có một vectơ chỉ phương \(\overrightarrow u = \left( {91;75;0} \right)\) có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 688 + 91t\\y = - 185 + 75t\\z = 8\end{array} \right.\) (t là tham số).
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vì B thuộc d nên B(-688 + 91t; -185 + 75t; 8).
Để B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa thì \(OB = 417\).
Do đó, \(\sqrt {{{\left( { - 688 + 91t} \right)}^2} + {{\left( { - 185 + 75t} \right)}^2} + {8^2}} = 417\)
\( \Leftrightarrow 13\;906{t^2} - 152\;966t + 333\;744 = 0\)\( \Leftrightarrow t = 3\) hoặc \(t = 8\).
Với \(t = 3\) ta có B(-415; 40; 8) và \(AB = \sqrt {{{\left( { - 415 + 688} \right)}^2} + {{\left( {40 + 185} \right)}^2}} = \sqrt {125\;154} \).
Với \(t = 8\) ta có B(40; 415; 8) và \(AB = \sqrt {{{\left( {40 + 688} \right)}^2} + {{\left( {415 + 185} \right)}^2}} = \sqrt {889\;984} \).
Vì \(\sqrt {125\;154} < \sqrt {889\;984} \) nên tọa độ vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là (-415; 40; 8).
b) Gọi H là vị trí mà máy bay gần đài kiểm soát không lưu nhất. Vì H thuộc d nên H(-688+91t’; -185+75t’;8).
Để OH là ngắn nhất khi và chỉ khi \(OH \bot d \Leftrightarrow \overrightarrow {OH} \bot \overrightarrow u \Leftrightarrow \overrightarrow {OH} .\overrightarrow u = 0\)
\( \Leftrightarrow \left( { - 688 + 91t'} \right).91 + \left( { - 185 + 75t'} \right).75 + 8.0 = 0 \Leftrightarrow 13\;906t' - 76\;483 = 0 \Leftrightarrow t' = \frac{{11}}{2}\).
Do đó, \(H\left( {\frac{{ - 375}}{2};\frac{{455}}{2};8} \right)\).
Khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó là:
\(OH = \sqrt {{{\left( {\frac{{ - 375}}{2}} \right)}^2} + {{\left( {\frac{{455}}{2}} \right)}^2} + {8^2}} = \frac{{\sqrt {347\;906} }}{2}\left( {km} \right)\).
c) Theo a ta có: tọa độ của vị trí mà máy bay ra khỏi màn hình ra đa là: (40; 415; 8).
Bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về... để giải quyết. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản, công thức liên quan và phương pháp giải phù hợp.
Đề bài yêu cầu chúng ta... Việc phân tích bài toán là bước đầu tiên và quan trọng nhất. Chúng ta cần xác định rõ các yếu tố đầu vào, đầu ra, các điều kiện ràng buộc và mục tiêu của bài toán. Từ đó, lựa chọn phương pháp giải phù hợp.
Để giải bài tập 14, chúng ta sẽ thực hiện các bước sau:
Cụ thể, ta có:
...
Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng xem xét một ví dụ minh họa:
Ví dụ: ...
Ngoài ra, các em có thể luyện tập thêm với các bài tập tương tự sau:
Khi giải bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh diều, các em cần lưu ý những điều sau:
Kiến thức về... không chỉ quan trọng trong việc giải bài tập mà còn có ứng dụng rộng rãi trong thực tế. Ví dụ, ...
Bài tập 14 trang 89 SGK Toán 12 tập 2 - Cánh diều là một bài tập thú vị và hữu ích, giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán. Để học tốt môn Toán, các em cần thường xuyên luyện tập, tìm hiểu các phương pháp giải khác nhau và tham khảo các nguồn tài liệu uy tín.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.
| STT | Nội dung |
|---|---|
| 1 | Khái niệm... |
| 2 | Công thức... |
Chúc các em học tập tốt!