Lý Thuyết Nguyên Hàm Toán 12 Cánh Diều

Lý thuyết Nguyên hàm của một hàm số sơ cấp Toán 12 Cánh Diều

Chào mừng bạn đến với bài học lý thuyết Nguyên hàm của một hàm số sơ cấp trong chương trình Toán 12 Cánh Diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng để hiểu và giải quyết các bài toán tích phân.

Chúng ta sẽ cùng nhau khám phá định nghĩa nguyên hàm, các tính chất của nguyên hàm và các phương pháp tìm nguyên hàm của các hàm số sơ cấp thường gặp.

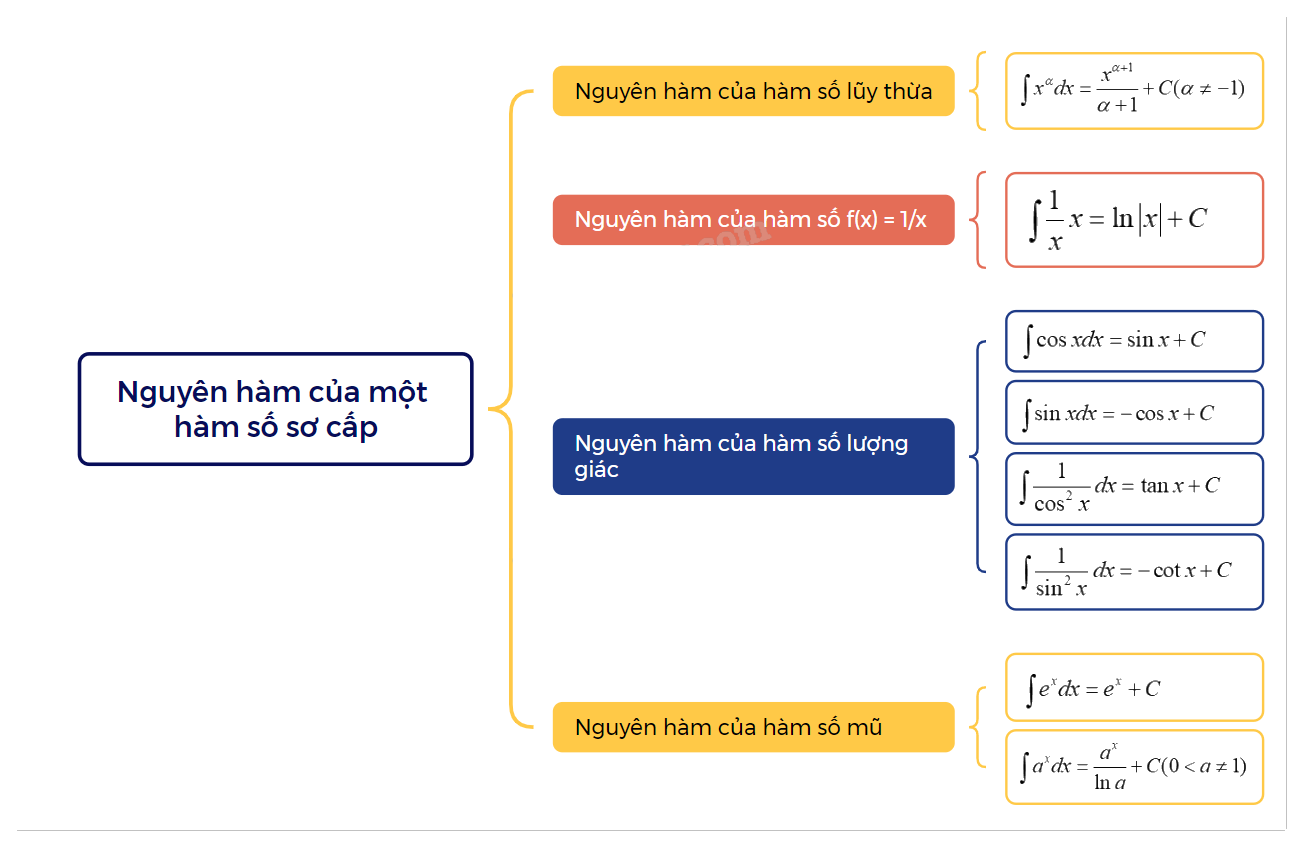
1. Nguyên hàm của hàm số lũy thừa Hàm số lũy thừa \(y = {x^\alpha }(\alpha \in R)\) có đạo hàm với mọi x > 0 và \(({x^\alpha })' = \alpha {x^{\alpha - 1}}\) \(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \)

1. Nguyên hàm của hàm số lũy thừa

Hàm số lũy thừa \(y = {x^\alpha }(\alpha \in R)\) có đạo hàm với mọi x > 0 và \(({x^\alpha })' = \alpha {x^{\alpha - 1}}\)

\(\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1)} \)

2. Nguyên hàm của hàm số \(f(x) = \frac{1}{x}\)

\(\int {\frac{1}{x}x = \ln \left| x \right| + C} \)

3. Nguyên hàm của hàm số lượng giác

\(\int {\cos xdx = \sin x + C} \)
\(\int {\sin xdx = - \cos x + C} \)
\(\int {\frac{1}{{{{\cos }^2}x}}dx = \tan x + C} \)
\(\int {\frac{1}{{{{\sin }^2}x}}dx = - \cot x + C} \)

4. Nguyên hàm của hàm số mũ

\(\int {{e^x}dx = {e^x} + C} \)
\(\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1)} \)

Lý thuyết Nguyên hàm của một hàm số sơ cấp Toán 12 Cánh Diều 1

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Lý thuyết Nguyên hàm của một hàm số sơ cấp Toán 12 Cánh Diều đặc sắc thuộc chuyên mục đề thi toán 12 trên nền tảng tài liệu toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Lý Thuyết Nguyên Hàm của Một Hàm Số Sơ Cấp Toán 12 Cánh Diều

Nguyên hàm là một khái niệm quan trọng trong giải tích, đóng vai trò then chốt trong việc giải quyết các bài toán tích phân. Hiểu rõ lý thuyết nguyên hàm là nền tảng để học tốt chương trình Toán 12 và các ứng dụng thực tế.

1. Định Nghĩa Nguyên Hàm

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên khoảng I nếu F'(x) = f(x) với mọi x thuộc I. Ký hiệu: ∫f(x)dx = F(x) + C, trong đó C là hằng số tích phân.

2. Tính Chất của Nguyên Hàm

Nếu F(x) là một nguyên hàm của f(x) thì F(x) + C cũng là một nguyên hàm của f(x) với mọi hằng số C.
Hàm số f(x) có vô số nguyên hàm, chúng khác nhau ở hằng số tích phân.
∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g(x)dx
∫kf(x)dx = k∫f(x)dx (với k là hằng số)

3. Nguyên Hàm của Một Số Hàm Số Sơ Cấp Thường Gặp

Dưới đây là bảng tổng hợp nguyên hàm của một số hàm số sơ cấp thường gặp:

Hàm số f(x)	Nguyên hàm F(x)
xⁿ (n ≠ -1)	(xⁿ⁺¹)/(n+1) + C
1/x	ln\|x\| + C
e^x	e^x + C
sin(x)	-cos(x) + C
cos(x)	sin(x) + C
1/(1+x²)	arctan(x) + C

4. Phương Pháp Tìm Nguyên Hàm

Có nhiều phương pháp để tìm nguyên hàm của một hàm số, trong đó phổ biến nhất là:

Phương pháp đặt ẩn phụ: Sử dụng để đơn giản hóa biểu thức tích phân.
Phương pháp tích phân từng phần: Áp dụng cho các tích phân có dạng ∫u dv. Công thức: ∫u dv = uv - ∫v du
Phương pháp phân tích thành nhân tử: Sử dụng để tách tích phân thành các tích phân đơn giản hơn.

5. Ví Dụ Minh Họa

Ví dụ 1: Tìm ∫(2x + 3)dx

Giải:

∫(2x + 3)dx = ∫2xdx + ∫3dx = 2∫xdx + 3∫dx = 2(x²/2) + 3x + C = x² + 3x + C

Ví dụ 2: Tìm ∫x*e^xdx (sử dụng tích phân từng phần)

Giải:

Đặt u = x, dv = e^xdx. Khi đó du = dx, v = e^x.

∫x*e^xdx = x*e^x - ∫e^xdx = x*e^x - e^x + C

6. Ứng Dụng của Nguyên Hàm

Nguyên hàm có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác, bao gồm:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
Tính thể tích vật thể.
Giải các bài toán vật lý liên quan đến chuyển động và công.

Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Nguyên hàm của một hàm số sơ cấp Toán 12 Cánh Diều. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.