Chào mừng các em học sinh đến với lời giải chi tiết bài tập 7 trang 14 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập 7 thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về giới hạn của hàm số. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là vô cùng quan trọng để các em đạt kết quả tốt trong các kỳ thi sắp tới.
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm (t = 0left( s right)) cho đến khi tên lửa đẩy được phóng đi tại thời điểm (t = 126left( s right)), cho bởi hàm số sau: (vleft( t right) = 0,001320{t^3} - 0,09029{t^2} + 23). (v được tính bằng ft/s, 1 feet = 0,3048 m) Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đế
Đề bài
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm \(t = 0\left( s \right)\) cho đến khi tên lửa đẩy được phóng đi tại thời điểm \(t = 126\left( s \right)\), cho bởi hàm số sau:
\(v\left( t \right) = 0,001302{t^3} - 0,09029{t^2} + 23\).
(v được tính bằng ft/s, 1 feet = 0,3048 m)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Phương pháp giải - Xem chi tiết
B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(a\left(t\right)=v'\left( t \right) = 3 \times 0,001302{t^2} - 2 \times 0,09029t\)
\(a'(t) = 7,{812.10^{ - 3}}t - 0,18058\)
Nhận xét \(a'\left( t \right) = 0 \Leftrightarrow t \approx 23,1\).
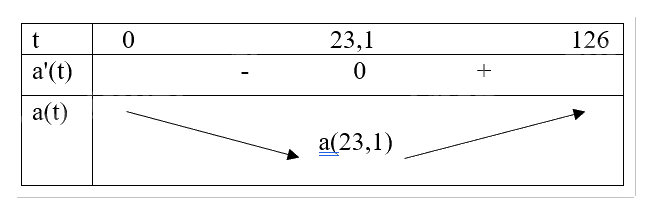
Vậy gia tốc tàu con thoi tăng từ giây thứ \(23,1\) đến giây thứ 126.
Bài tập 7 trang 14 SGK Toán 12 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để tính toán và chứng minh các biểu thức toán học. Đây là một bài tập quan trọng giúp củng cố lý thuyết và rèn luyện kỹ năng giải toán.
Bài tập 7 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập 7 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi của bài tập 7:
Để tính giới hạn của hàm số tại một điểm, ta có thể sử dụng định nghĩa giới hạn hoặc các định lý về giới hạn. Trong trường hợp này, ta có thể sử dụng định lý về giới hạn của thương để tính giới hạn.
Ví dụ:
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x + 2) = 4
Để chứng minh sự tồn tại của giới hạn, ta cần chứng minh rằng giới hạn bên trái và giới hạn bên phải của hàm số tại điểm đó bằng nhau.
Ví dụ:
lim (x→0+) x^2 = 0 và lim (x→0-) x^2 = 0. Do đó, lim (x→0) x^2 = 0
Để sử dụng các định lý về giới hạn, ta cần biến đổi biểu thức về dạng đơn giản hơn. Ví dụ, ta có thể nhân tử và mẫu của phân thức với một biểu thức thích hợp để khử các yếu tố gây khó khăn trong việc tính giới hạn.
Khi giải bài tập 7, học sinh cần lưu ý những điều sau:
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học, bao gồm:
Bài tập 7 trang 14 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong các kỳ thi sắp tới.
Chúc các em học tập tốt!