Giải bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Cánh diều. Bài viết này sẽ giúp bạn giải quyết triệt để bài tập 11 trang 47, nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả tốt nhất.

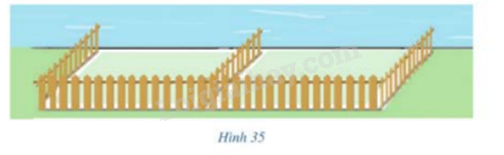
Một người nông dân có 15.000.000 đồng để làm một hàng rào hình cữ E dọc theo một con sông bao quanh hai khu đất trông lúa có dạng hai hình chữ nhật bằng nhau(hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60.000/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000đồng/ mét, mặt giáp với bờ soog không phải hàng rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào

Đề bài

Một người nông dân có 15.000.000 đồng để làm một hàng rào hình chữ E dọc theo một con sông bao quanh hai khu đất trông lúa có dạng hai hình chữ nhật bằng nhau (hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng/mét, mặt giáp với bờ sông không phải hàng rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.

Giải bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều 1

Phương pháp giải - Xem chi tiết Giải bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều 2

Phân tích đề bài.

Tìm các mối quan hệ trong bài.

Lập phương trình và giải.

Lời giải chi tiết

Giả sử chiều dài từng mặt của ba mặt hàng rào song song nhau là x (m).

Chi phí để làm ba mặt hàng rào song song là: 3.x.50000 = 150000x (đồng).

Chi phí để làm mặt hàng rào song song với bờ sông là: 15000000 – 150000x (đồng).

Chiều dài của mặt hàng rào song song với bờ sông là \(\frac{{15000000 - 150000x}}{{60000}} = \frac{{1500 - 15x}}{6}\) (m).

Điều kiện: \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{1500 - 15x > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 0}\\{x < 100}\end{array}} \right.\)

Giả sử diện tích hàng rào không đáng kể, khi đó diện tích hai khu đất thu được sau khi làm hàng rào là:

\(S(x) = \frac{{x(1500 - 15x)}}{6} = \frac{{ - 15{x^2} + 1500x}}{6}\) (\({m^2}\)).

Diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào là giá trị lớn nhất của hàm số S(x).

Xét \(S'(x) = - \frac{{15}}{3}x + \frac{{1500}}{6} = 0 \Leftrightarrow x = 50\).

Ta có bảng biến thiên:

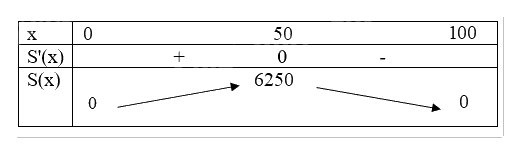
Giải bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều 3

Trên khoảng (0;100), hàm số S(x) đạt giá trị lớn nhất bằng 6250 tại x = 50.

Vậy diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào là 6250 \({m^2}\).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều đặc sắc thuộc chuyên mục đề thi toán 12 trên nền tảng đề thi toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều: Tổng quan

Bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.

Nội dung bài tập 11 trang 47

Bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều thường có dạng như sau: Cho một hàm số y = f(x). Tính đạo hàm f'(x) tại một điểm x cụ thể hoặc tìm đạo hàm của hàm số trên một khoảng xác định. Đôi khi, bài tập còn yêu cầu học sinh sử dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số, hoặc các bài toán tối ưu hóa.

Phương pháp giải bài tập 11 trang 47

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số y = f(x) cần xét.
Chọn công thức đạo hàm phù hợp: Dựa vào dạng của hàm số, chọn công thức đạo hàm tương ứng. Ví dụ, nếu hàm số là đa thức, ta sử dụng công thức đạo hàm của đa thức. Nếu hàm số là hàm lượng giác, ta sử dụng công thức đạo hàm của hàm lượng giác.
Tính đạo hàm: Áp dụng công thức đạo hàm đã chọn để tính đạo hàm f'(x).
Thay giá trị x: Nếu bài toán yêu cầu tính đạo hàm tại một điểm x cụ thể, thay giá trị x vào biểu thức f'(x) để tìm kết quả.
Kiểm tra lại kết quả: Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa

Ví dụ: Cho hàm số y = x³ - 2x² + 5x - 1. Tính đạo hàm f'(x).

Giải:

Áp dụng công thức đạo hàm của đa thức, ta có:

f'(x) = 3x² - 4x + 5

Các dạng bài tập thường gặp

Đạo hàm của hàm số đơn thức: Ví dụ: y = xⁿ, y = axⁿ
Đạo hàm của hàm số đa thức: Ví dụ: y = x³ + 2x² - x + 1
Đạo hàm của hàm số lượng giác: Ví dụ: y = sin(x), y = cos(x), y = tan(x)
Đạo hàm của hàm số mũ và logarit: Ví dụ: y = e^x, y = ln(x)
Đạo hàm của hàm hợp: Ví dụ: y = sin(x²)

Lưu ý khi giải bài tập

Nắm vững các công thức đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Kiểm tra lại kết quả sau khi tính toán.
Sử dụng máy tính bỏ túi để hỗ trợ tính toán.

Bài tập luyện tập

Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:

Tính đạo hàm của hàm số y = 2x⁴ - 3x² + 7.
Tính đạo hàm của hàm số y = sin(2x) + cos(x).
Tính đạo hàm của hàm số y = e^x + ln(x).

Kết luận

Bài tập 11 trang 47 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và vận dụng kiến thức vào giải quyết các bài toán thực tế. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.