Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2 trang 88 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài tập 2 trang 88 thuộc chương trình học Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của 1 công ty (đơn vị: triệu đồng) a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó
Đề bài
Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của 1 công ty (đơn vị: triệu đồng).
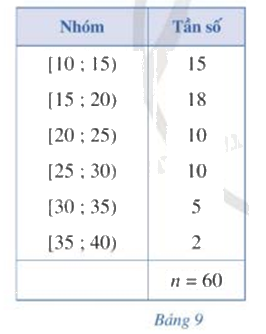
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
Phương pháp giải - Xem chi tiết
a) Khoảng biến thiên là hiệu của đầu mút phải nhóm cuối cùng và đầu mút trái nhóm đầu tiên.
b) Khoảng tứ phân vị là \({Q_3} - {Q_1}\).
Lời giải chi tiết
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = 40 - 10 = 30\).
b) Số phần tử của mẫu là n = 60.
Tần số tích lũy của các nhóm lần lượt là \(c{f_1} = 15\), \(c{f_2} = 33\), \(c{f_3} = 43\), \(c{f_4} = 53\), \(c{f_5} = 58\), \(c{f_6} = 60\).
Ta có: \(\frac{n}{4} = \frac{{60}}{4} = 15\) suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 15. Xét nhóm 1 là nhóm [10;15] có s = 10, h = 5, \({n_1} = 15\).
Ta có tứ phân vị thứ nhất là: \({Q_1} = s + \left( {\frac{{15 - c{f_0}}}{{{n_1}}}} \right).h = 10 + \left( {\frac{{15 - 0}}{{15}}} \right).5 = 15\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.60}}{4} = 45\) mà 43 < 45 < 53 suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 45. Xét nhóm 4 là nhóm [25;30] có t = 25, l = 5, \({n_4} = 10\)và nhóm 3 là nhóm [20;25] có \(c{f_3} = 43\).
Ta có tứ phân vị thứ ba là: \({Q_3} = t + \left( {\frac{{45 - c{f_3}}}{{{n_4}}}} \right).l = 25 + \left( {\frac{{45 - 43}}{{10}}} \right).5 = 26\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: \({Q_3} - {Q_1} = 26 - 15 = 11\).
Bài tập 2 trang 88 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các vấn đề thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Bài tập 2 thường bao gồm các dạng bài sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập 2 trang 88 SGK Toán 12 tập 1 - Cánh diều, chúng tôi xin trình bày lời giải chi tiết cho từng dạng bài:
Lời giải:
y' = 3x2 - 4x + 5
Lời giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Để giải bài tập 2 trang 88 SGK Toán 12 tập 1 - Cánh diều một cách nhanh chóng và chính xác, các em có thể tham khảo một số mẹo sau:
Ngoài SGK Toán 12 tập 1 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã trình bày, các em học sinh sẽ tự tin hơn khi giải bài tập 2 trang 88 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt!