Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 84,85 SGK Toán 12 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập này thuộc chương trình Toán 12 tập 1, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Khoảng biến thiên
Đề bài
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 12 Cánh diều
Xét mẫu số liệu ghép nhóm cho bởi Bảng 2.
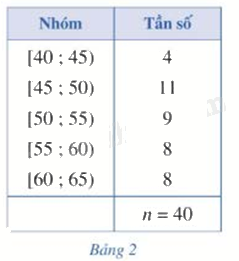
a) Tìm \({a_1},{a_6}\) lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm 5
b) Tính hiệu \(R = {a_6} - {a_1}\)
Phương pháp giải - Xem chi tiết
Quan sát bảng số liệu
Lời giải chi tiết
a) \({a_1} = 40\); \({a_6} = 65\)
b) \(R = {a_6} - {a_1} = 65 - 40 = 15\)
Mục 1 trang 84,85 SGK Toán 12 tập 1 - Cánh diều tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến khảo sát hàm số. Các bài tập trong mục này thường yêu cầu học sinh xác định khoảng đồng biến, nghịch biến, cực trị, và vẽ đồ thị hàm số. Việc nắm vững các khái niệm và kỹ năng này là vô cùng quan trọng để đạt kết quả tốt trong các kỳ thi sắp tới.
Bài tập này yêu cầu học sinh khảo sát hàm số bậc ba, bao gồm các bước sau:
Để giải bài tập này, học sinh cần nắm vững các công thức tính đạo hàm và các quy tắc tìm cực trị. Ngoài ra, việc vẽ đồ thị hàm số cũng đòi hỏi sự chính xác và tỉ mỉ.
Bài tập này yêu cầu học sinh khảo sát hàm số hữu tỉ, bao gồm các bước tương tự như bài tập 1. Tuy nhiên, việc xác định tập xác định và các điểm bất thường của hàm số hữu tỉ có thể phức tạp hơn.
Học sinh cần chú ý đến các điểm gián đoạn của hàm số và xét giới hạn của hàm số tại các điểm này.
Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số trong một khoảng cho trước.
Để giải bài tập này, học sinh cần phân tích bài toán, xây dựng hàm số mô tả bài toán, và sử dụng đạo hàm để tìm ra lời giải.
Để giải các bài tập trong mục 1 trang 84,85 SGK Toán 12 tập 1 - Cánh diều một cách hiệu quả, học sinh nên:
Xét hàm số y = x3 - 3x2 + 2. Ta thực hiện các bước khảo sát hàm số như sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Việc học toán đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian ôn tập lý thuyết và luyện tập bài tập thường xuyên. Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè. Chúc các em học tập tốt!