Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 10 trang 80 SGK Toán 12 tập 2 theo chương trình Cánh diều, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu và phù hợp với nhu cầu của học sinh, sinh viên.
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S. ABCD có các đỉnh lần lượt là (Sleft( {0;0;frac{{asqrt 3 }}{2}} right),Aleft( {frac{a}{2};0;0} right),Bleft( { - frac{a}{2};0;0} right),Cleft( { - frac{a}{2};a;0} right),Dleft( {frac{a}{2};a;0} right)) với (a > 0) (Hình 36).
Đề bài
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S. ABCD có các đỉnh lần lượt là \(S\left( {0;0;\frac{{a\sqrt 3 }}{2}} \right),A\left( {\frac{a}{2};0;0} \right),B\left( { - \frac{a}{2};0;0} \right),C\left( { - \frac{a}{2};a;0} \right),D\left( {\frac{a}{2};a;0} \right)\) với \(a > 0\) (Hình 36).
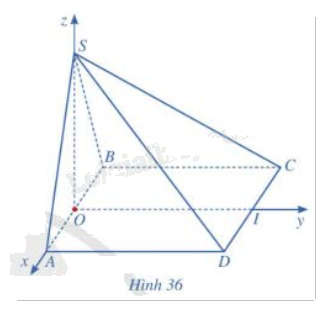
a) Xác định tọa độ của các vectơ \(\overrightarrow {SA} ,\overrightarrow {CD} \). Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).
b) Chỉ ra một vectơ pháp tuyến của mặt phẳng (SAC). Từ đó tính góc đường thẳng SD và mặt phẳng (SAC) (làm tròn kết quả đến hàng đơn vị của độ).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về côsin góc giữa hai đường thẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right)\), \(\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó, ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\)
b) Sử dụng kiến thức về côsin góc giữa đường thẳng và mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {{a_1};{b_1};{c_1}} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {{a_2};{b_2};{c_2}} \right)\). Gọi \(\left( {\Delta ,\left( P \right)} \right)\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\).
Lời giải chi tiết
a) Ta có: \(\overrightarrow {SA} = \left( {\frac{a}{2};0;\frac{{ - a\sqrt 3 }}{2}} \right),\overrightarrow {CD} = \left( {a;0;0} \right)\).
Do đó, \(\cos \left( {SA,CD} \right) = \frac{{\left| {\frac{a}{2}.a + 0.0 - \frac{{a\sqrt 3 }}{2}.0} \right|}}{{\sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {0^2} + {{\left( {\frac{{ - a\sqrt 3 }}{2}} \right)}^2}} .\sqrt {{a^2} + {0^2} + {0^2}} }} = \frac{1}{2}\) nên \(\left( {SA,CD} \right) = {60^o}\).
b) Mặt phẳng (SAC) nhận \(\left[ {\overrightarrow {SA} ,\overrightarrow {AC} } \right]\) làm một vectơ pháp tuyến.
Ta có: \(\overrightarrow {SA} = \left( {\frac{a}{2};0;\frac{{ - a\sqrt 3 }}{2}} \right),\overrightarrow {AC} = \left( { - a;a;0} \right),\overrightarrow {SD} = \left( {\frac{a}{2};a;\frac{{ - a\sqrt 3 }}{2}} \right)\).
\(\left[ {\overrightarrow {SA} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{\frac{{ - a\sqrt 3 }}{2}}\\a&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\frac{{ - a\sqrt 3 }}{2}}&{\frac{a}{2}}\\0&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\frac{a}{2}}&0\\{ - a}&a\end{array}} \right|} \right) = \left( {\frac{{{a^2}\sqrt 3 }}{2};\frac{{{a^2}\sqrt 3 }}{2};\frac{{{a^2}}}{2}} \right)\)
Do đó, \(\sin \left( {\left( {SAC} \right),SD} \right) = \frac{{\left| {\frac{{{a^2}\sqrt 3 }}{2}.\frac{a}{2} + \frac{{{a^2}\sqrt 3 }}{2}.a + \frac{{{a^2}}}{2}.\frac{{ - a\sqrt 3 }}{2}} \right|}}{{\sqrt {{{\left( {\frac{{{a^2}\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{{a^2}\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{{a^2}}}{2}} \right)}^2}} \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {a^2} + {{\left( {\frac{{ - a\sqrt 3 }}{2}} \right)}^2}} }} = \frac{{\sqrt {42} }}{{14}}\).
Suy ra, \(\left( {\left( {SAC} \right),SD} \right) \approx {28^o}\).
Bài tập 10 trang 80 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp để giải quyết các bài toán cụ thể. Việc nắm vững các quy tắc đạo hàm và kỹ năng biến đổi đại số là rất quan trọng để hoàn thành bài tập này một cách hiệu quả.
Bài tập 10 thường bao gồm các dạng bài sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lưu ý rằng, trong quá trình giải bài, bạn cần:
Câu hỏi: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
Áp dụng quy tắc đạo hàm của tổng, hiệu, và lũy thừa, ta có:
f'(x) = 3x2 + 4x - 5
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Ngoài SGK Toán 12 tập 2 - Cánh diều, bạn có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về đạo hàm:
Hy vọng rằng, với những hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả, bạn sẽ tự tin hơn trong việc giải bài tập 10 trang 80 SGK Toán 12 tập 2 - Cánh diều và các bài tập đạo hàm khác. Chúc bạn học tập tốt!