Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 12 tập 1 - Cánh diều. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp dễ hiểu nhất.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn bộ giải đáp này để giúp các bạn học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Sơ đồ khảo sát hàm số
Đề bài
Trả lời câu hỏi Hoạt động trang 28SGK Toán 12 Cánh diều
Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 2x - 3\).
Phương pháp giải - Xem chi tiết
-Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
Lời giải chi tiết
-Tập xác định: \(\mathbb{R}\)
-Sự biến thiên:
Giới hạn tại vô cực : \(\mathop {\lim }\limits_{x \to + \infty } = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
\(y{\rm{'}} = 2x - 2\)
\(y{\rm{'}} = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\)
Bảng biến thiên
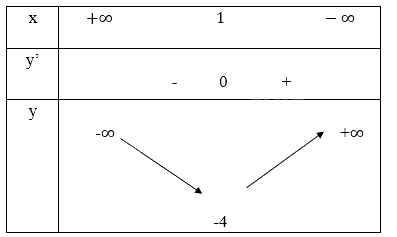
Vẽ đồ thị hàm số
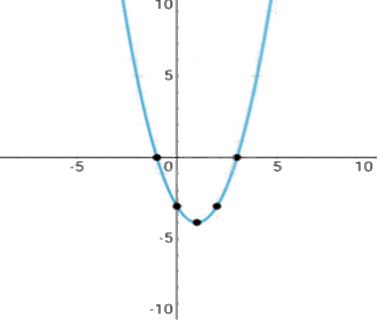
Trang 28 SGK Toán 12 tập 1 - Cánh diều tập trung vào các bài tập liên quan đến giới hạn của hàm số. Đây là một trong những khái niệm nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc hiểu các khái niệm nâng cao hơn như đạo hàm và tích phân. Việc nắm vững phương pháp giải các bài tập về giới hạn sẽ giúp học sinh xây dựng nền tảng vững chắc cho các kiến thức tiếp theo.
Trang 28 bao gồm các bài tập rèn luyện kỹ năng tính giới hạn của hàm số tại một điểm và khi x tiến tới vô cùng. Các dạng bài tập thường gặp bao gồm:
a) lim (x→2) (x^2 - 4) / (x - 2)
Giải: Ta có thể phân tích tử số thành (x - 2)(x + 2). Khi đó, biểu thức trở thành lim (x→2) (x + 2). Thay x = 2 vào, ta được kết quả là 4.
b) lim (x→-1) (x^3 + 1) / (x + 1)
Giải: Tương tự, ta phân tích tử số thành (x + 1)(x^2 - x + 1). Khi đó, biểu thức trở thành lim (x→-1) (x^2 - x + 1). Thay x = -1 vào, ta được kết quả là 3.
a) lim (x→∞) (2x + 1) / (x - 3)
Giải: Chia cả tử số và mẫu số cho x, ta được lim (x→∞) (2 + 1/x) / (1 - 3/x). Khi x tiến tới vô cùng, 1/x và 3/x tiến tới 0. Do đó, giới hạn bằng 2/1 = 2.
b) lim (x→∞) (x^2 + 1) / (x^2 + 2x + 3)
Giải: Chia cả tử số và mẫu số cho x^2, ta được lim (x→∞) (1 + 1/x^2) / (1 + 2/x + 3/x^2). Khi x tiến tới vô cùng, 1/x^2, 2/x và 3/x^2 tiến tới 0. Do đó, giới hạn bằng 1/1 = 1.
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác. Ví dụ, giới hạn được sử dụng để định nghĩa đạo hàm, tích phân, và các khái niệm quan trọng khác trong giải tích. Ngoài ra, giới hạn còn được sử dụng trong các bài toán về vật lý, kinh tế, và thống kê.
Việc giải các bài tập trang 28 SGK Toán 12 tập 1 - Cánh diều là một bước quan trọng trong quá trình học tập môn Toán của các bạn học sinh. Hy vọng rằng với hướng dẫn chi tiết và các lưu ý trên, các bạn sẽ tự tin hơn trong việc giải quyết các bài tập về giới hạn và nắm vững kiến thức nền tảng cho các chương trình học tiếp theo.