Chào mừng các em học sinh đến với lời giải chi tiết bài tập 7 trang 44 SGK Toán 12 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 7 thuộc chương trình học Toán 12 tập 1, tập trung vào việc rèn luyện kỹ năng về...
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250km so với bề mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm độ cao hát của con tàu so với bề mặt của mặt trăng được tính gần đúng bởi hàm. (hleft( t right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250) Trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét a) Vẽ đồ thị của hàm số (y = hleft( t right)) với (0{rm{ }} le t le {rm{ }
Đề bài
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250km so với bề mặt của Mặt Trăng.
Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm độ cao hát của con tàu so với bề mặt của mặt trăng được tính gần đúng bởi hàm:
\(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\)
Trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét.
a) Tìm thời điểm t (0 ≤ t ≤ 70) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
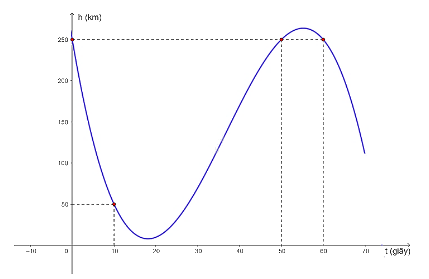
b) Vẽ đồ thị của hàm số y = h(t) với 0 ≤ t ≤ 70 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km).
c) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤ 70. Xác định hàm số v(t).
d) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?
e) Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
Phương pháp giải - Xem chi tiết
Ứng dụng đạo hàm trong xử lý các bài toán thực tiễn.
Lời giải chi tiết
a) Xét hàm số \( h(t) = -0,01t^3 + 1,1t^2 - 30t + 250 \) với \( t \in [0; 70] \).
Ta có \( h'(t) = -0,03t^2 + 2,2t - 30 \);
Trên khoảng (0; 70), \( h'(t) = 0 \) khi \( t \approx 18 \) hoặc \( t \approx 55 \).
\( h(0) = 250; h(18) \approx 8,08; h(55,23) \approx 263,75; h(70) = 110 \).
Do đó, \(\min_{[0; 70]} h(t) = 8,08 \) tại \( t = 18 \).
Vậy tại thời điểm \( t = 18 \) giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.
b) Xét hàm số \( h(t) = -0,01t^3 + 1,1t^2 - 30t + 250 \) với \( t \in [0; 70] \).
Ta có \( h'(t) = -0,03t^2 + 2,2t - 30 \);
Trên khoảng (0; 70), \( h'(t) = 0 \) khi \( t \approx 18 \) hoặc \( t \approx 55 \).
Bảng biến thiên của hàm số \( h(t) \) như sau:
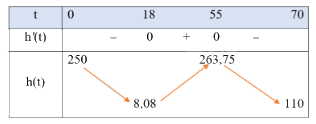
Trên khoảng (0; 70), đồ thị hàm số h(t) đi qua các điểm (0; 250), (10; 50), (50; 250) và (60; 250).
c) Ta có \(v(t)\) là vận tốc tức thời của con tàu ở thời điểm \(t\) (giây) kể từ khi đốt cháy các tên lửa hãm với \(0 \le t \le 70\).
Khi đó \(v(t) = h'(t) = -0,03t^2 + 2,2t - 30\) với \(t \in [0; 70]\).
d) Tại thời điểm bắt đầu đốt cháy các tên lửa hãm, tức \(t = 0\), vận tốc của tức thời của con tàu là:
\(v(0) = -0,03 \cdot 0^2 + 2,2 \cdot 0 - 30 = -30\) (km/s).
Tại thời điểm \(t = 25\) (giây), vận tốc tức thời của con tàu là:
\(v(25) = -0,03 \cdot 25^2 + 2,2 \cdot 25 - 30 = 6,25\) (km/s).
e) Tại thời điểm \(t = 25\) (giây), lúc đó \(t \in (18; 55)\), căn cứ vào bảng biến thiên ở câu b), ta thấy rằng \(h'(t) > 0\), tức là \(v(t) > 0\), vậy vận tốc tức thời của con tàu đang tăng trở lại.
Bài tập 7 trang 44 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn thường gặp.
Đề bài yêu cầu chúng ta tính giới hạn của hàm số tại một điểm cho trước. Việc phân tích đề bài cẩn thận là bước đầu tiên quan trọng để xác định phương pháp giải phù hợp. Cần xác định rõ hàm số, điểm cần tính giới hạn và các yếu tố có thể ảnh hưởng đến quá trình tính toán.
Có nhiều phương pháp để giải bài tập 7 trang 44, tùy thuộc vào dạng hàm số và điểm cần tính giới hạn. Dưới đây là một số phương pháp phổ biến:
Bài tập: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn, các em có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về giới hạn, các em cần lưu ý những điều sau:
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, như:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập 7 trang 44 SGK Toán 12 tập 1 - Cánh diều này, các em sẽ hiểu rõ hơn về kiến thức về giới hạn và tự tin hơn trong quá trình học tập. Chúc các em học tốt!