Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Cánh diều. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 5 trang 43, từ đó nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả tốt nhất.
khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau: (a,;y = 2{x^3} - 3x + 1 b,;y = - {x^3} + 3x - 1) c, ( y = {left( {x - 2} right)^3} + 4) d,(y = - {x^3} + 3{x^2} - 1) e, (y = frac{1}{3}{x^3} + {x^2} + 2x + 1) g,( y = - {x^3} - 3x)
Đề bài
khảo sát về sự biến thiên và vẽ đồ thị của các hàm số sau:
a,\(y = 2{x^3} - 3{x^2} + 1\)
b,\(y = - {x^3} + 3{x^2} - 1\)
c, \( y = {\left( {x - 2} \right)^3} + 4\)
d,\(y = - {x^3} + 3{x^2} - 3x + 2\)
e, \(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1\)
g,\( y = - {x^3} - 3x\)
Phương pháp giải - Xem chi tiết
Tìm TXD
Xét sự biến thiên
Vẽ đồ thị
Lời giải chi tiết
a,
\(y = 2{x^3} - 3{x^2} + 1\)
Tập xác định: D = R
\(y' = 6{x^2}\) - 6x; y' = 0 \( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 0}\end{array}} \right.\)
Bảng biến thiên
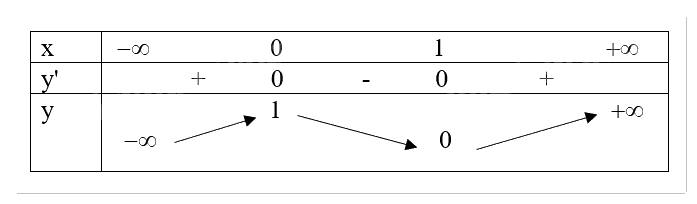
Đồ thị hàm số
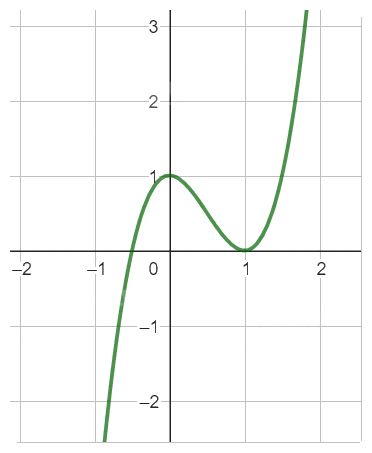
b,
\(y = - {x^3} + 3{x^2} - 1\)
Tập xác định: D = R
\(y' = - 3{x^2} + 6x\); y' = 0 \( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Bảng biến thiên
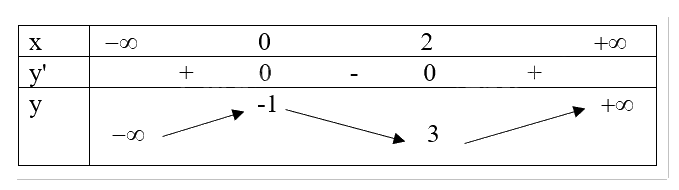
Đồ thị hàm số
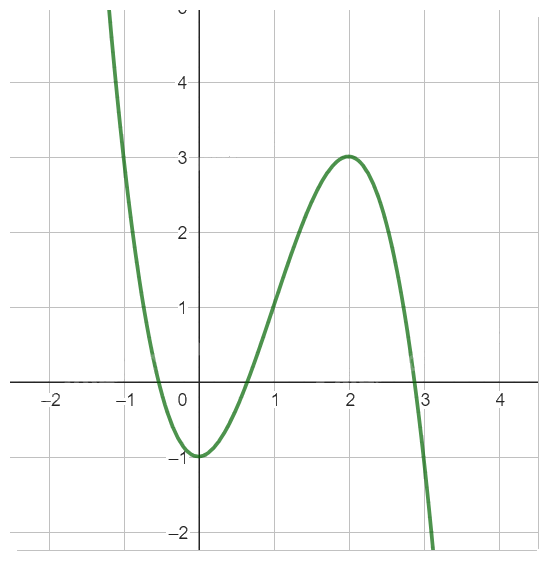
c,
\(y = {\left( {x - 2} \right)^3} + 4\)
Tập xác định: D = R
\(y' = 3{\left( {x - 2} \right)^2} \), y’=0 \( = > {\left( {x\;-\;2} \right)^2} = 0 = > x - 2 = 0 = > x = 2\)
Bảng biến thiên
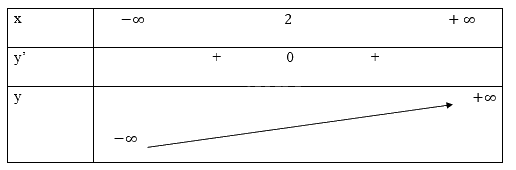
Đồ thị hàm số
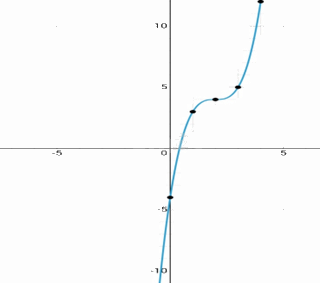
d,
\(y = - {x^3} + 3{x^2} - 3x + 2\)
Tập xác định: D = R
\(y' = - 3{x^2} + 6x - 3,\;y' = 0 = > x = 1\)
Bảng biến thiên:
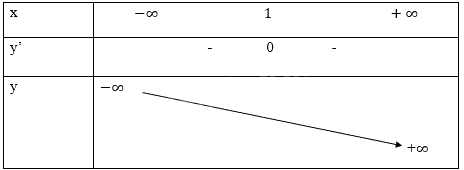
Đồ thị hàm số
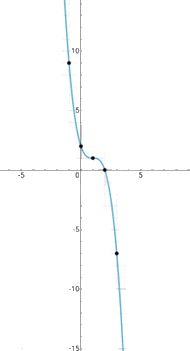
e,\(y = \frac{1}{3}{x^3} + {x^2} + 2x + 1 = > y' = {x^2} + 2x + 2 > 0, \forall x \in D\)
Tập xác định: D = R
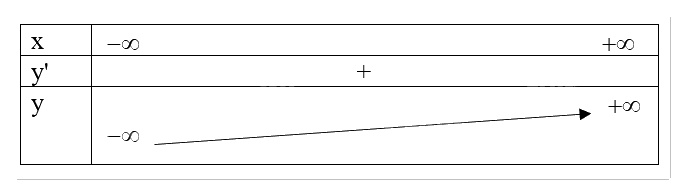
Đồ thị hàm số
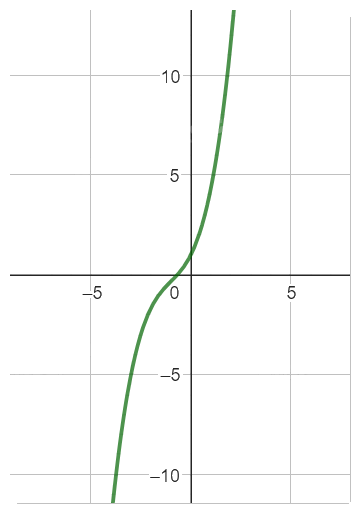
g,\(y = - {x^3} - 3x = > y' = - 3{x^2} - 3 < 0, \forall x \in D\)
Tập xác định: D = R
Bảng biến thiên
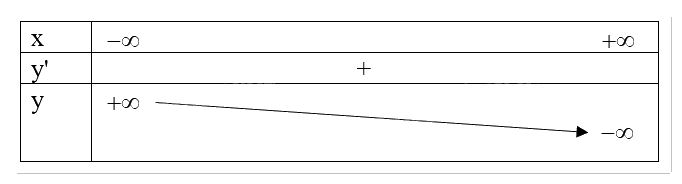
Đồ thị hàm số
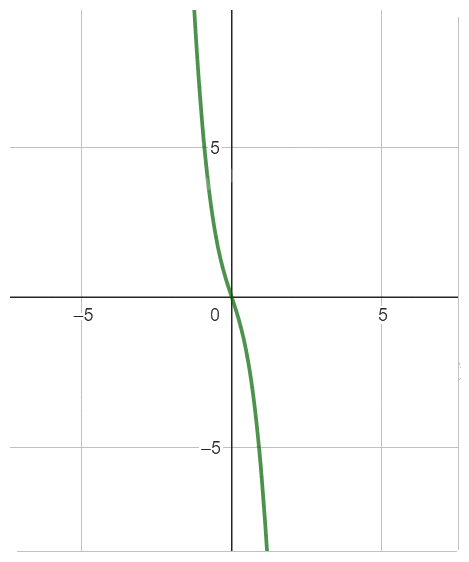
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 0}\end{array}} \right.\)
Bài tập 5 trang 43 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong các kỳ thi.
Bài tập 5 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ hoặc hàm lượng giác. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 5:
Để tính giới hạn của hàm số tại một điểm, ta có thể sử dụng phương pháp trực tiếp thay giá trị của điểm đó vào hàm số. Tuy nhiên, nếu việc thay trực tiếp dẫn đến dạng vô định, ta cần sử dụng các phương pháp khác như phân tích thành nhân tử, nhân liên hợp hoặc áp dụng quy tắc L'Hopital.
Ví dụ, nếu hàm số là f(x) = (x^2 - 1) / (x - 1), ta có thể phân tích thành nhân tử như sau: f(x) = (x - 1)(x + 1) / (x - 1). Khi đó, ta có thể rút gọn biểu thức thành f(x) = x + 1. Vậy, giới hạn của hàm số tại x = 1 là 1 + 1 = 2.
Tương tự như câu a, ta cần xác định đúng dạng của hàm số và áp dụng các quy tắc tính giới hạn phù hợp. Nếu hàm số là hàm hữu tỉ, ta cần kiểm tra xem mẫu số có bằng 0 tại điểm cần tính giới hạn hay không. Nếu mẫu số bằng 0, ta cần sử dụng các phương pháp khác để tính giới hạn.
Đối với các hàm số lượng giác, ta cần sử dụng các công thức lượng giác và các giới hạn đặc biệt để tính giới hạn. Ví dụ, ta có giới hạn lim (sin x) / x = 1 khi x tiến đến 0.
Ngoài bài tập 5, còn rất nhiều bài tập tương tự về giới hạn hàm số. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức sau:
Để học tập hiệu quả môn Toán 12, học sinh nên:
Bài tập 5 trang 43 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trên, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.
| Bài tập | Lời giải |
|---|---|
| Câu a | (Lời giải chi tiết câu a) |
| Câu b | (Lời giải chi tiết câu b) |
| Câu c | (Lời giải chi tiết câu c) |