Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau a,(y = {x^3} - 3{x^2} + 2) (b,;y = - {x^3} + 3{x^2} - 6x) (c,y = frac{{3x - 2}}{{x - 2}}) (d,y = frac{x}{{2x + 3}}) (e,y = frac{{{x^2} + 2x + 4}}{x}) (g,y = frac{{{x^2} + 4x + 3}}{{x + 2}};)
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau
a,\(y = {x^3} - 3{x^2} + 2\)
\(b,\;y = - {x^3} + 3{x^2} - 6x\)
\(c,y = \frac{{3x - 2}}{{x - 2}}\)
\(d,y = \frac{x}{{2x + 3}}\)
\(e,y = \frac{{{x^2} + 2x + 4}}{x}\)
\(g,y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;\)
Phương pháp giải - Xem chi tiết
Tìm tập xác định
Vẽ bảng biến thiên
Vẽ đồ thị
Lời giải chi tiết
\(a,\;y = {x^3} - 3{x^2} + 2\)
TXD : R
\(y' = 3{x^2} - 6x\)
Cho y= 0 => \(\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Bảng biến thiên:
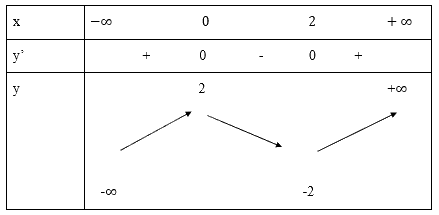
Đồ thị hàm số:
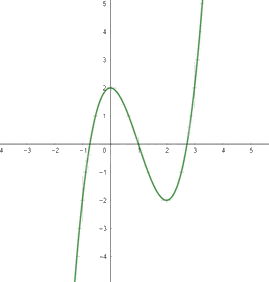
Hàm số đồng biến trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\)
Hàm số nghịch biến trong khoảng (0;2)
\(\;b,\;y = - {x^3} + 3{x^2} - 6x\)
TXD: R
\(y' = \; - 3{x^2} + 6x - 6\)
Bảng biến thiên:
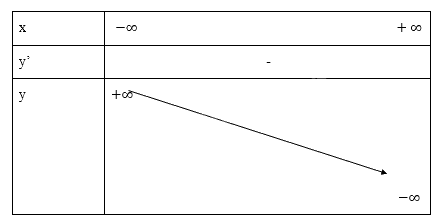
Đồ thị hàm số
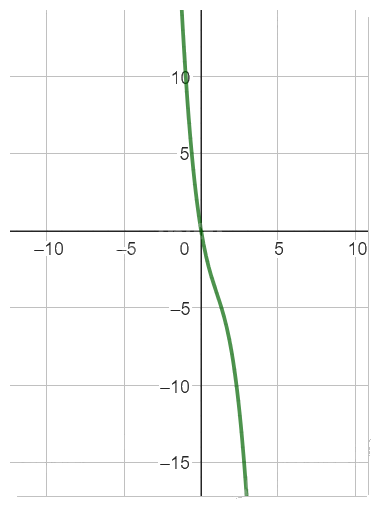
Hàm số nghịch biến trên R
\(c,y = \frac{{3x - 2}}{{x - 2}}\)
TXD: R/2
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x - 2}} = 3 = > TCN\;y = 3\)
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{3x - 2}}{{x - 2}} = - \infty \)
Bảng biến thiên:
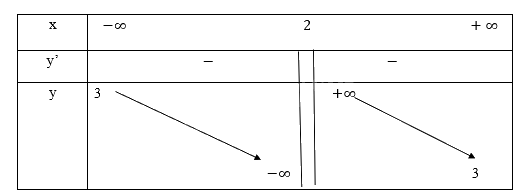
Đồ thị hàm số:
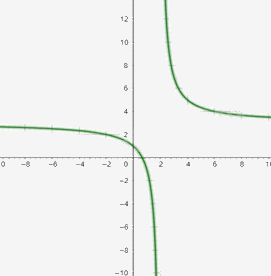
Hàm số nghịch biến trên khoảng R
\(d,y = \frac{x}{{2x + 3}}\)
TXD: R \ {\( - \frac{3}{2}\)}
TCN \(y = \frac{1}{2}\)
TCD \(x = - \frac{3}{2}\)
Bảng biến thiên
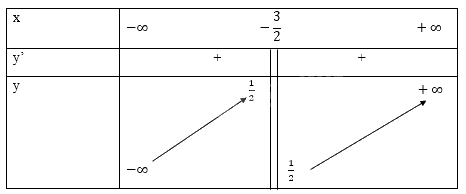
Đồ thị hàm số:
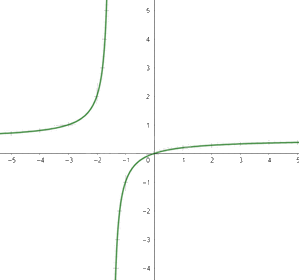
\(e,y = \frac{{{x^2} + 2x + 4}}{x}\)
\(TXD:\mathbb{R}\backslash \{ 0\} \)
TCD: x = 0.
Không có tiệm cận ngang.
Có thể viết hàm số đã cho dưới dạng: \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 + \frac{4}{x}\), suy ra:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{x} = 0.\\\mathop {\lim }\limits_{x \to - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{4}{x} = 0.\end{array}\)
Do đó, đồ thị hàm số có \(y = x + 2\) là tiệm cận xiên.
\(y' = \frac{{\left( {2x + 2} \right)x - \left( {{x^2} + 2x + 4} \right)}}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}\).
Cho y’=0 => x=\( \pm 2\).
Bảng biến thiên:
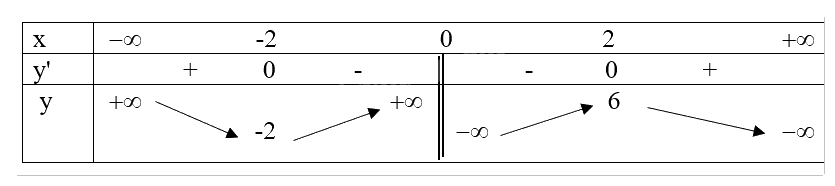
Đồ thị hàm số:
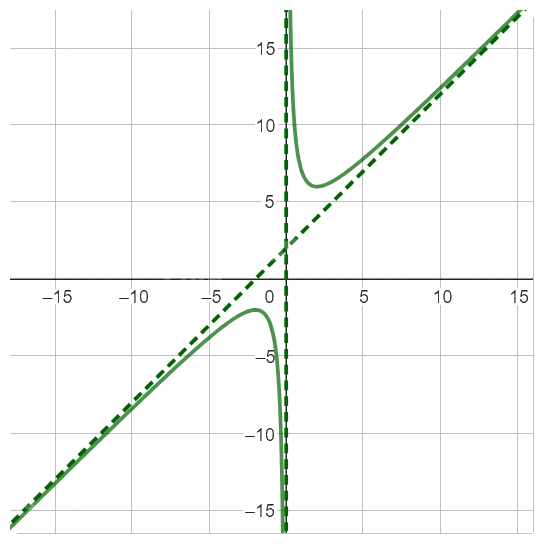
g, \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\)
TXD: \(\mathbb{R}\backslash \{ - 2\} \). \[\]
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \). Đồ thị àm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to - {2^ - }} y = + \infty \). Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng.
Có thể viết hàm số đã cho dưới dạng: \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 - \frac{1}{{x + 2}}\), suy ra:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{x + 2}} = 0.\\\mathop {\lim }\limits_{x \to - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{x + 2}} = 0.\end{array}\)
Do đó, đồ thị hàm số có \(y = x + 2\) là tiệm cận xiên.
Bảng biến thiên:
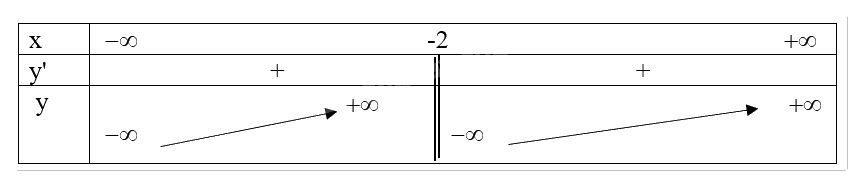
Đồ thị hàm số:
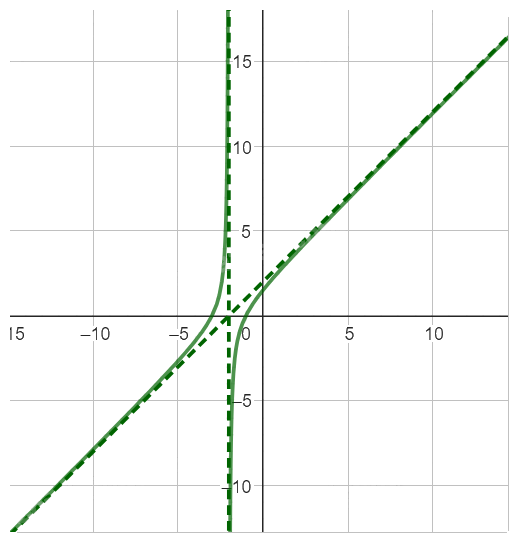
Bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại vô cùng để giải quyết các bài toán cụ thể. Việc nắm vững các định nghĩa, tính chất và các phương pháp tính giới hạn là yếu tố then chốt để hoàn thành bài tập này.
Bài tập 9 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể hoặc khi x tiến tới vô cùng. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số phức tạp hơn. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi của bài tập 9:
Để giải câu a, ta cần tính giới hạn của hàm số khi x tiến tới một giá trị cụ thể. Ta có thể sử dụng phương pháp thay trực tiếp giá trị của x vào hàm số. Nếu kết quả là một số thực, thì đó là giới hạn của hàm số. Nếu kết quả là một dạng vô định, ta cần sử dụng các phương pháp khác để tính giới hạn.
Đối với câu b, ta cần tính giới hạn của hàm số khi x tiến tới vô cùng. Ta có thể sử dụng phương pháp chia cả tử và mẫu cho x. Khi đó, ta sẽ thu được một biểu thức đơn giản hơn, dễ dàng tính giới hạn.
Câu c có thể yêu cầu học sinh sử dụng các công thức giới hạn đặc biệt, chẳng hạn như giới hạn của (sin x)/x khi x tiến tới 0. Việc nắm vững các công thức này sẽ giúp học sinh giải quyết bài tập một cách nhanh chóng và chính xác.
Để củng cố kiến thức về giới hạn, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 1 - Cánh diều và các tài liệu ôn tập khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi giải các bài tập về giới hạn.
Bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn. Hy vọng rằng với lời giải chi tiết và các phương pháp hướng dẫn trong bài viết này, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!