Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
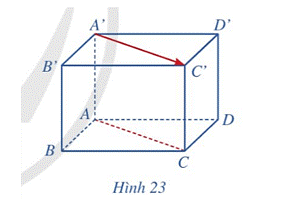
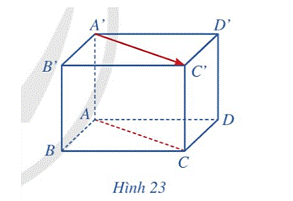
Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ (overrightarrow {A'C'} ) và đường thẳng AC có vị trí tương đối như thế nào?
Trả lời câu hỏi Luyện tập 2 trang 67 SGK Toán 12 Cánh diều
Viết phương trình tham số của đường thẳng \(\Delta \), biết \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) và vuông góc với mặt phẳng (P): \(3x - y + 2z - 1 = 0\).
Phương pháp giải:
Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
Mặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n \left( {3; - 1;2} \right)\).
Vì đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) nên đường thẳng \(\Delta \) nhận \(\overrightarrow n \left( {3; - 1;2} \right)\) làm một vectơ chỉ phương.
Lại có, \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) nên phương trình tham số của đường thẳng \(\Delta \) là: \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 - t\\z = - 4 + 2t\end{array} \right.\) (t là tham số).
Trả lời câu hỏi Hoạt động 3 trang 67 SGK Toán 12 Cánh diều
Cho đường thẳng \(\Delta \) có phương trình tham số:
\(\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 + 7t\\z = 5 + 8t\end{array} \right.\) (t là tham số).
Tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) có thỏa mãn hệ phương trình \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\) hay không?
Phương pháp giải:
Sử dụng kiến thức về phương trình tham số của đường thẳng để trả lời câu hỏi: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
Vì M (x; y; z) nằm trên \(\Delta \) nên \(\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 + 7t\\z = 5 + 8t\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}t = \frac{{x - 2}}{3}\\t = \frac{{y - 4}}{7}\\t = \frac{{z - 5}}{8}\end{array} \right.\). Do đó, \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\).
Do đó, điểm M(x; y; z) nằm trên \(\Delta \) thỏa mãn hệ phương trình \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\).
Trả lời câu hỏi Hoạt động 4 trang 68 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {1;2;3} \right)\) và \(B\left( {3;5;9} \right)\).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng AB.
c) Viết phương trình chính tắc của đường thẳng AB.
Phương pháp giải:
+ Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
+ Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình chính tắc của đường thẳng: Nếu \(abc \ne 0\) thì hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
a) Một vectơ chỉ phương của đường thẳng AB là \(\overrightarrow {AB} = \left( {2;3;6} \right)\).
b) Đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;6} \right)\).
Mà đường thẳng AB đi qua điểm \(A\left( {1;2;3} \right)\) nên phương trình tham số của đường thẳng AB là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + 3t\\z = 3 + 6t\end{array} \right.\) (t là tham số).
c) Phương trình chính tắc của đường thẳng AB là: \(\frac{{x - 1}}{2} = \frac{{y - 2}}{3} = \frac{{z - 3}}{6}\).
Trả lời câu hỏi Luyện tập 3 trang 68 SGK Toán 12 Cánh diều
Viết phương trình chính tắc đường thẳng \(\Delta \), biết phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3 - 5t\\z = 6 + 9t\end{array} \right.\) (t là tham số).
Phương pháp giải:
Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình chính tắc của đường thẳng: Nếu \(abc \ne 0\) thì hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
Đường thẳng \(\Delta \) đi qua \(M\left( { - 1;3;6} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 5;9} \right)\) nên phương trình chính tắc của đường thẳng \(\Delta \) là: \(\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z - 6}}{9}\).
Trả lời câu hỏi Luyện tập 4 trang 69 SGK Toán 12 Cánh diều
Viết phương trình chính tắc của đường thẳng OM biết M(a; b; c) với \(abc \ne 0\).
Phương pháp giải:
Sử dụng kiến thức về lập phương trình chính tắc của đường thẳng đi qua hai điểm để viết phương trình: Đường thẳng \(\Delta \) đi qua hai điểm \(A\left( {{x_0};{y_0};{z_0}} \right),B\left( {{x_1};{y_1};{z_1}} \right)\) có phương trình chính tắc là: \(\frac{{x - {x_0}}}{{{x_1} - {x_0}}} = \frac{{y - {y_0}}}{{{y_1} - {y_0}}} = \frac{{z - {z_0}}}{{{z_1} - {z_0}}}\) (với \({x_0} \ne {x_1};{y_0} \ne {y_1};{z_0} \ne {z_1}\)).
Lời giải chi tiết:
Phương trình chính tắc của đường thẳng OM là: \(\frac{{x - 0}}{a} = \frac{{y - 0}}{b} = \frac{{z - 0}}{c} \Leftrightarrow \frac{x}{a} = \frac{y}{b} = \frac{z}{c}\).
Trả lời câu hỏi Luyện tập 1 trang 65 SGK Toán 12 Cánh diều
Trong Hình 23, vectơ \(\overrightarrow {B'D'} \) có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?
Phương pháp giải:
Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {B'D'} \) là đường thẳng B’D’. Mà BD//B’D’ (do ABCD.A’B’C’D’ là hình hộp) nên vectơ \(\overrightarrow {B'D'} \) là vectơ chỉ phương của đường thẳng BD.
Trả lời câu hỏi Hoạt động 2 trang 66 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {1;2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 3;5} \right)\). Xét điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) nằm trên \(\Delta \) (Hình 24).
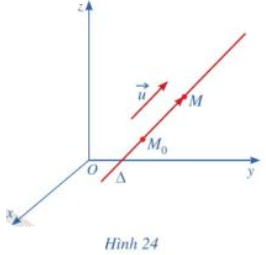
a) Nêu nhận xét về phương của hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \).
b) Có hay không số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \)?
c) Hãy biểu diễn x, y, z qua t.
d) Tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) có thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 3t\\z = 3 + 5t\end{array} \right.\) hay không?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau.
b) Vì hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau nên tồn tại số thực t khác 0 sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \).
c) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - 1;y - 2;z - 3} \right)\).
Theo b ta có: \(\overrightarrow {{M_o}M} = t\overrightarrow u \) nên \(\left\{ \begin{array}{l}x - 1 = 2t\\y - 2 = - 3t\\z - 3 = 5t\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = 2t + 1\\y = - 3t + 2\\z = 5t + 3\end{array} \right.\).
d) Vì \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) và theo b ta có \(\left\{ \begin{array}{l}x = 2t + 1\\y = - 3t + 2\\z = 5t + 3\end{array} \right.\) nên tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 3t\\z = 3 + 5t\end{array} \right.\).
Trả lời câu hỏi Hoạt động 1 trang 65 SGK Toán 12 Cánh diều
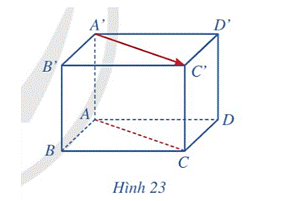
Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ \(\overrightarrow {A'C'} \) và đường thẳng AC có vị trí tương đối như thế nào?
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {A'C'} \) là đường thẳng A’C’. Mà AC//A’C’ (do ABCD.A’B’C’D’ là hình hộp) nên giá của vectơ \(\overrightarrow {A'C'} \) song song đường thẳng AC.
Trả lời câu hỏi Hoạt động 1 trang 65 SGK Toán 12 Cánh diều
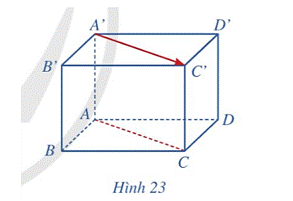
Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ \(\overrightarrow {A'C'} \) và đường thẳng AC có vị trí tương đối như thế nào?
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {A'C'} \) là đường thẳng A’C’. Mà AC//A’C’ (do ABCD.A’B’C’D’ là hình hộp) nên giá của vectơ \(\overrightarrow {A'C'} \) song song đường thẳng AC.
Trả lời câu hỏi Luyện tập 1 trang 65 SGK Toán 12 Cánh diều
Trong Hình 23, vectơ \(\overrightarrow {B'D'} \) có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?
Phương pháp giải:
Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {B'D'} \) là đường thẳng B’D’. Mà BD//B’D’ (do ABCD.A’B’C’D’ là hình hộp) nên vectơ \(\overrightarrow {B'D'} \) là vectơ chỉ phương của đường thẳng BD.
Trả lời câu hỏi Hoạt động 2 trang 66 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {1;2;3} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 3;5} \right)\). Xét điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) nằm trên \(\Delta \) (Hình 24).
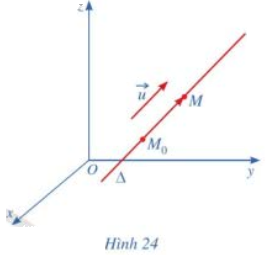
a) Nêu nhận xét về phương của hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \).
b) Có hay không số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \)?
c) Hãy biểu diễn x, y, z qua t.
d) Tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) có thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 3t\\z = 3 + 5t\end{array} \right.\) hay không?
Phương pháp giải:
+ Sử dụng kiến thức về giá của vectơ trong không gian để trả lời: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ.
+ Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để trả lời: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \) . Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).
Lời giải chi tiết:
a) Hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau.
b) Vì hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau nên tồn tại số thực t khác 0 sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \).
c) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - 1;y - 2;z - 3} \right)\).
Theo b ta có: \(\overrightarrow {{M_o}M} = t\overrightarrow u \) nên \(\left\{ \begin{array}{l}x - 1 = 2t\\y - 2 = - 3t\\z - 3 = 5t\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = 2t + 1\\y = - 3t + 2\\z = 5t + 3\end{array} \right.\).
d) Vì \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) và theo b ta có \(\left\{ \begin{array}{l}x = 2t + 1\\y = - 3t + 2\\z = 5t + 3\end{array} \right.\) nên tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 3t\\z = 3 + 5t\end{array} \right.\).
Trả lời câu hỏi Luyện tập 2 trang 67 SGK Toán 12 Cánh diều
Viết phương trình tham số của đường thẳng \(\Delta \), biết \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) và vuông góc với mặt phẳng (P): \(3x - y + 2z - 1 = 0\).
Phương pháp giải:
Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
Mặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n \left( {3; - 1;2} \right)\).
Vì đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) nên đường thẳng \(\Delta \) nhận \(\overrightarrow n \left( {3; - 1;2} \right)\) làm một vectơ chỉ phương.
Lại có, \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) nên phương trình tham số của đường thẳng \(\Delta \) là: \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 - t\\z = - 4 + 2t\end{array} \right.\) (t là tham số).
Trả lời câu hỏi Hoạt động 3 trang 67 SGK Toán 12 Cánh diều
Cho đường thẳng \(\Delta \) có phương trình tham số:
\(\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 + 7t\\z = 5 + 8t\end{array} \right.\) (t là tham số).
Tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) có thỏa mãn hệ phương trình \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\) hay không?
Phương pháp giải:
Sử dụng kiến thức về phương trình tham số của đường thẳng để trả lời câu hỏi: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
Vì M (x; y; z) nằm trên \(\Delta \) nên \(\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 + 7t\\z = 5 + 8t\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}t = \frac{{x - 2}}{3}\\t = \frac{{y - 4}}{7}\\t = \frac{{z - 5}}{8}\end{array} \right.\). Do đó, \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\).
Do đó, điểm M(x; y; z) nằm trên \(\Delta \) thỏa mãn hệ phương trình \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\).
Trả lời câu hỏi Luyện tập 3 trang 68 SGK Toán 12 Cánh diều
Viết phương trình chính tắc đường thẳng \(\Delta \), biết phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3 - 5t\\z = 6 + 9t\end{array} \right.\) (t là tham số).
Phương pháp giải:
Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình chính tắc của đường thẳng: Nếu \(abc \ne 0\) thì hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
Đường thẳng \(\Delta \) đi qua \(M\left( { - 1;3;6} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 5;9} \right)\) nên phương trình chính tắc của đường thẳng \(\Delta \) là: \(\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z - 6}}{9}\).
Trả lời câu hỏi Hoạt động 4 trang 68 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {1;2;3} \right)\) và \(B\left( {3;5;9} \right)\).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng AB.
c) Viết phương trình chính tắc của đường thẳng AB.
Phương pháp giải:
+ Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
+ Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình chính tắc của đường thẳng: Nếu \(abc \ne 0\) thì hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\).
Lời giải chi tiết:
a) Một vectơ chỉ phương của đường thẳng AB là \(\overrightarrow {AB} = \left( {2;3;6} \right)\).
b) Đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;6} \right)\).
Mà đường thẳng AB đi qua điểm \(A\left( {1;2;3} \right)\) nên phương trình tham số của đường thẳng AB là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + 3t\\z = 3 + 6t\end{array} \right.\) (t là tham số).
c) Phương trình chính tắc của đường thẳng AB là: \(\frac{{x - 1}}{2} = \frac{{y - 2}}{3} = \frac{{z - 3}}{6}\).
Trả lời câu hỏi Luyện tập 4 trang 69 SGK Toán 12 Cánh diều
Viết phương trình chính tắc của đường thẳng OM biết M(a; b; c) với \(abc \ne 0\).
Phương pháp giải:
Sử dụng kiến thức về lập phương trình chính tắc của đường thẳng đi qua hai điểm để viết phương trình: Đường thẳng \(\Delta \) đi qua hai điểm \(A\left( {{x_0};{y_0};{z_0}} \right),B\left( {{x_1};{y_1};{z_1}} \right)\) có phương trình chính tắc là: \(\frac{{x - {x_0}}}{{{x_1} - {x_0}}} = \frac{{y - {y_0}}}{{{y_1} - {y_0}}} = \frac{{z - {z_0}}}{{{z_1} - {z_0}}}\) (với \({x_0} \ne {x_1};{y_0} \ne {y_1};{z_0} \ne {z_1}\)).
Lời giải chi tiết:
Phương trình chính tắc của đường thẳng OM là: \(\frac{{x - 0}}{a} = \frac{{y - 0}}{b} = \frac{{z - 0}}{c} \Leftrightarrow \frac{x}{a} = \frac{y}{b} = \frac{z}{c}\).
Mục 1 của SGK Toán 12 tập 2 - Cánh diều tập trung vào các kiến thức về Đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 12, là nền tảng cho việc giải quyết nhiều bài toán phức tạp hơn trong các chương tiếp theo. Việc nắm vững các khái niệm, định lý và kỹ năng liên quan đến đạo hàm là điều cần thiết để đạt kết quả tốt trong kỳ thi THPT Quốc gia.
Chúng ta sẽ cùng nhau đi qua từng bài tập trong mục 1, từ trang 65 đến trang 69, để hiểu rõ cách áp dụng các kiến thức đã học vào thực tế. Mỗi bài tập sẽ được phân tích kỹ lưỡng, kèm theo lời giải chi tiết và các lưu ý quan trọng.
Các bài tập đầu tiên trên trang 65 thường tập trung vào việc kiểm tra lại các khái niệm cơ bản về đạo hàm. Các em cần nắm vững định nghĩa đạo hàm, quy tắc tính đạo hàm của các hàm số đơn giản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
Các bài tập trên trang 66 thường yêu cầu các em áp dụng các quy tắc tính đạo hàm phức tạp hơn, như quy tắc tích, quy tắc thương, quy tắc hàm hợp. Các em cần chú ý đến việc xác định đúng các hàm số thành phần và áp dụng đúng quy tắc tương ứng.
Các bài tập từ trang 67 đến trang 69 thường là các bài tập ứng dụng đạo hàm để giải quyết các bài toán thực tế, như tìm cực trị của hàm số, khảo sát hàm số, giải phương trình, bất phương trình. Các em cần kết hợp kiến thức về đạo hàm với các kiến thức khác đã học để giải quyết các bài toán này.
Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!