Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1 - Cánh diều, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 9, 10, 11 của SGK Toán 12 tập 1 - Cánh diều. Các lời giải được trình bày một cách rõ ràng, logic, kèm theo các ví dụ minh họa cụ thể.
Điểm cực trị, giá trị cực trị của hàm số
Trả lời câu hỏi Hoạt động 3 trang 9 SGK Toán 12 Cánh diều
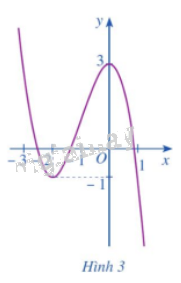
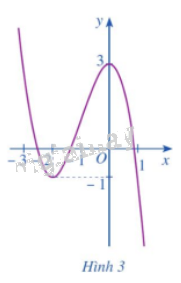
Dựa vào đồ thị hàm số \(y = f\left( x \right) = - {x^3} - 3{x^2} + 3\) ở Hình 3, hãy so sánh:
a) \(f\left( { - 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).
Phương pháp giải:
Dựa vào đồ thị hàm số
Lời giải chi tiết:
a) Nhận xét: Ta thấy rằng \(f\left( x \right) > f\left( { - 2} \right)\) với mọi \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) Tương tự: Ta thấy rằng \(f\left( x \right) < f\left( 0 \right)\) với mọi \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).
Trả lời câu hỏi Luyện tập 5 trang 11 SGK Toán 12 Cánh diều
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^4} - 32x + 1\).
b) \(y = \frac{{3x + 5}}{{x - 1}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} - 32\).
Xét \(y' = 0 \Leftrightarrow x = 2 \).
Ta có bảng biến thiên sau:
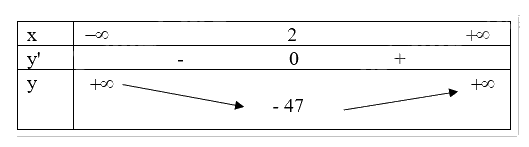
Vậy hàm số đạt cực tiểu tại điểm \(x = 2\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y' = \frac{{ - 8}}{{{{\left( {x - 1} \right)}^2}}}\).
Nhận xét \(y' < 0{\rm{ }}\forall x \in D\)
Ta có bảng biến thiên sau:
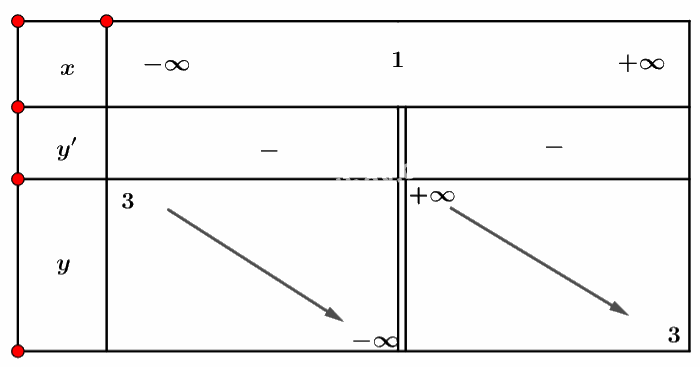
Vậy hàm số không có điểm cực trị.
Trả lời câu hỏi Hoạt động 4 trang 10 SGK Toán 12 Cánh diều
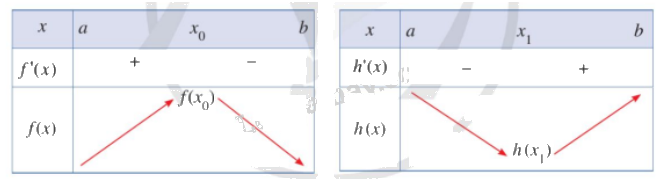
Quan sát bảng biến thiên dưới đây và cho biết:
a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) hay không.
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\) hay không.
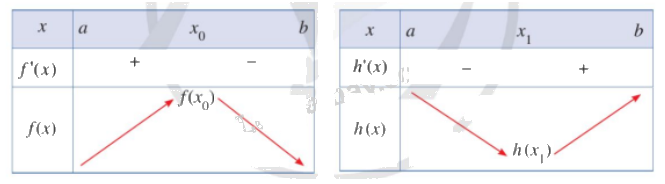
Phương pháp giải:
Dựa vào Bảng biến thiên và định nghĩa điểm cực tiểu của hàm số
Lời giải chi tiết:
a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) .
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\).
Trả lời câu hỏi Hoạt động 3 trang 9 SGK Toán 12 Cánh diều
Dựa vào đồ thị hàm số \(y = f\left( x \right) = - {x^3} - 3{x^2} + 3\) ở Hình 3, hãy so sánh:
a) \(f\left( { - 2} \right)\) với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) \(f\left( 0 \right)\)với mỗi giá trị \(f\left( x \right)\), ở đó \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).
Phương pháp giải:
Dựa vào đồ thị hàm số
Lời giải chi tiết:
a) Nhận xét: Ta thấy rằng \(f\left( x \right) > f\left( { - 2} \right)\) với mọi \(x \in \left( { - 3; - 1} \right)\) và \(x \ne - 2\).
b) Tương tự: Ta thấy rằng \(f\left( x \right) < f\left( 0 \right)\) với mọi \(x \in \left( { - 1;1} \right)\) và \(x \ne 0\).
Trả lời câu hỏi Hoạt động 4 trang 10 SGK Toán 12 Cánh diều
Quan sát bảng biến thiên dưới đây và cho biết:
a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) hay không.
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\) hay không.
Phương pháp giải:
Dựa vào Bảng biến thiên và định nghĩa điểm cực tiểu của hàm số
Lời giải chi tiết:
a) \({x_o}\) có là điểm cực đại của hàm số \(f\left( x \right)\) .
b) \({x_1}\) có là điểm cực tiểu của hàm số \(h\left( x \right)\).
Trả lời câu hỏi Luyện tập 5 trang 11 SGK Toán 12 Cánh diều
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^4} - 32x + 1\).
b) \(y = \frac{{3x + 5}}{{x - 1}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} - 32\).
Xét \(y' = 0 \Leftrightarrow x = 2 \).
Ta có bảng biến thiên sau:
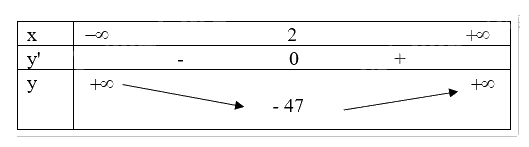
Vậy hàm số đạt cực tiểu tại điểm \(x = 2\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y' = \frac{{ - 8}}{{{{\left( {x - 1} \right)}^2}}}\).
Nhận xét \(y' < 0{\rm{ }}\forall x \in D\)
Ta có bảng biến thiên sau:
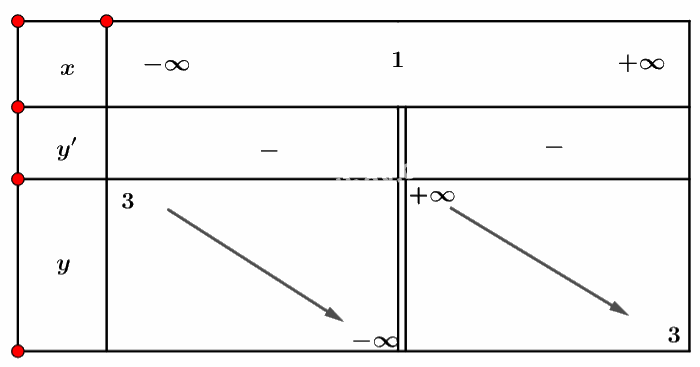
Vậy hàm số không có điểm cực trị.
Mục 2 của SGK Toán 12 tập 1 - Cánh diều tập trung vào việc ôn tập và mở rộng kiến thức về hàm số bậc hai. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán ở các lớp trên. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Các bài tập trên trang 9 thường yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, xác định đỉnh, trục đối xứng và giao điểm với các trục tọa độ. Để giải các bài tập này, học sinh cần nắm vững định nghĩa và các công thức liên quan.
Ví dụ: Cho hàm số y = x2 - 4x + 3. Xác định các hệ số a, b, c và tìm tọa độ đỉnh của parabol.
Lời giải:
Trang 10 tập trung vào việc khảo sát sự biến thiên của hàm số bậc hai và vẽ đồ thị. Để giải các bài tập này, học sinh cần xác định được các yếu tố quan trọng như đỉnh, trục đối xứng, giao điểm với các trục tọa độ và chiều của parabol.
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số y = -x2 + 2x + 1.
Lời giải:
Các bài tập trên trang 11 thường yêu cầu học sinh ứng dụng kiến thức về hàm số bậc hai để giải các bài toán thực tế. Các bài toán này có thể liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc giải các bài toán tối ưu hóa.
Ví dụ: Một người nông dân muốn rào một mảnh đất hình chữ nhật có diện tích 100m2. Hỏi người đó cần sử dụng bao nhiêu mét hàng rào để rào mảnh đất đó với chi phí thấp nhất?
Lời giải:
Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là x và y. Ta có diện tích S = xy = 100. Chu vi của mảnh đất là P = 2(x + y). Ta cần tìm giá trị nhỏ nhất của P. Từ S = xy = 100, ta có y = 100/x. Thay vào P, ta được P = 2(x + 100/x). Để tìm giá trị nhỏ nhất của P, ta xét hàm số f(x) = x + 100/x. Đạo hàm f'(x) = 1 - 100/x2. Giải phương trình f'(x) = 0, ta được x = 10. Khi x = 10, y = 100/10 = 10. Vậy mảnh đất hình chữ nhật có chu vi nhỏ nhất khi x = y = 10. Chu vi nhỏ nhất là P = 2(10 + 10) = 40m.
Hy vọng với những lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều. Chúc các em học tập tốt!