Chuyên đề Ứng dụng hình học của tích phân trong chương trình Toán 12 Cánh Diều là một phần quan trọng, giúp học sinh vận dụng kiến thức tích phân vào giải quyết các bài toán thực tế về diện tích và thể tích.
Tại giaitoan.edu.vn, chúng tôi cung cấp hệ thống lý thuyết đầy đủ, dễ hiểu, cùng với các ví dụ minh họa chi tiết, giúp bạn nắm vững kiến thức nền tảng và kỹ năng giải bài tập.
1.Tính diện tích hình phẳng a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
1.Tính diện tích hình phẳng
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \) |
b) Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = f(x), g(x) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng x = a, x = b được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \) |
2. Tính thể tích của hình khối
Cho một vật thể trong không gian Oxyz. Gọi \(\beta \) là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm có hoành độ x = a, x = b. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích là S(x). Giả sử S(x) là hàm số liên tục trên đoạn \(\left[ {a;b} \right]\). Khi đó thể tích V của vật thể \(\beta \) được tính bởi công thức \(V = \int\limits_a^b {S(x)dx} \) |
b) Thể tích của khối tròn xoay
Cho hàm số f(x) liên tục, không âm trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b xung quanh trục hoành, ta được hình khối gọi là một khối tròn xoay. Khi cắt khối tròn xoay đó bởi một mặt phẳng vuông góc với trục Ox tại điểm \(x \in \left[ {a;b} \right]\) được một hình tròn có bán kính f(x). Thể tích của khối tròn xoay này là: \(V = \pi \int\limits_a^b {{f^2}(x)dx} \)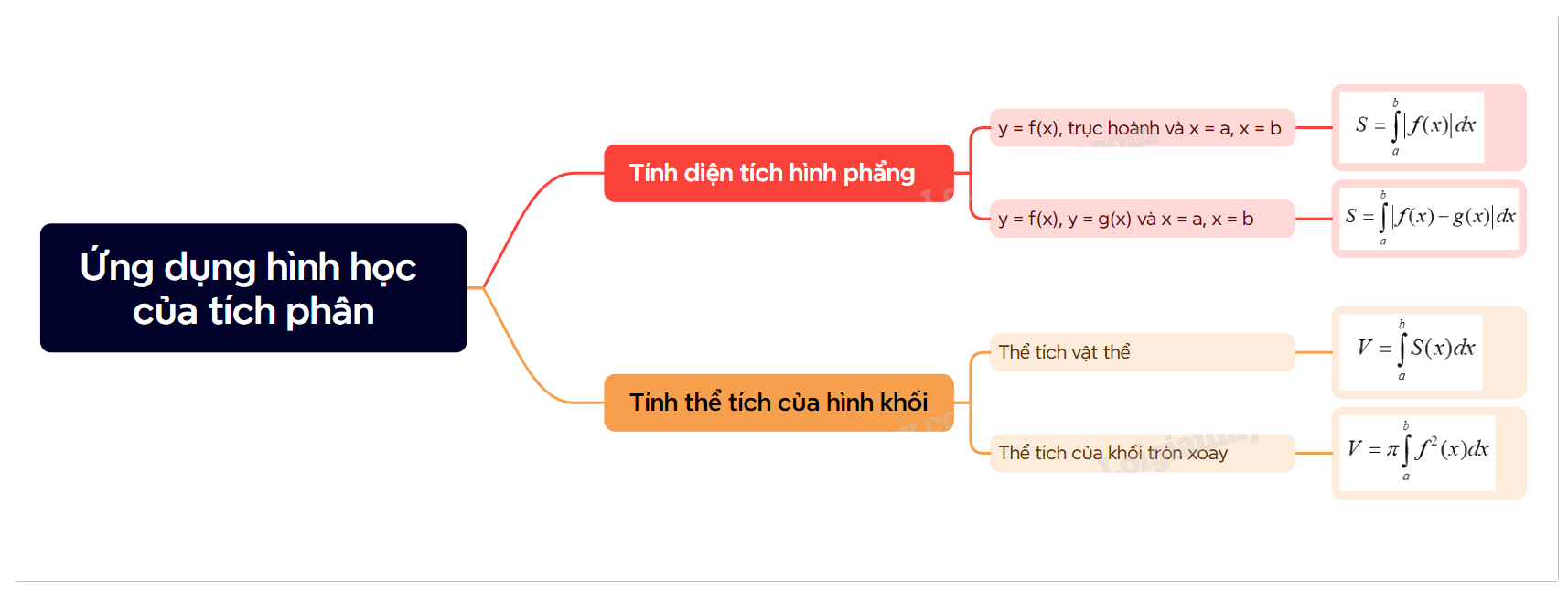 |
Ứng dụng hình học của tích phân là một trong những nội dung trọng tâm của chương trình Toán 12, đặc biệt trong sách giáo khoa Cánh Diều. Chuyên đề này tập trung vào việc sử dụng tích phân để tính diện tích hình phẳng và thể tích vật thể. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến ứng dụng hình học của tích phân là rất quan trọng để đạt kết quả tốt trong các kỳ thi.
Để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành Ox và hai đường thẳng x = a, x = b (với a < b), ta sử dụng công thức:
S = ∫ab |f(x)| dx
Trong đó:
Nếu f(x) ≥ 0 trên [a, b] thì |f(x)| = f(x). Nếu f(x) ≤ 0 trên [a, b] thì |f(x)| = -f(x).
Có nhiều phương pháp để tính thể tích vật thể bằng tích phân, tùy thuộc vào hình dạng của vật thể. Một số phương pháp phổ biến bao gồm:
Các bài tập về ứng dụng hình học của tích phân thường yêu cầu:
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đường cong y = x2, trục hoành Ox và hai đường thẳng x = -1, x = 2.
Giải:
Diện tích hình phẳng là:
S = ∫-12 |x2| dx = ∫-12 x2 dx = [x3/3]-12 = (8/3) - (-1/3) = 3
Ví dụ 2: Tính thể tích vật thể tròn xoay khi quay miền phẳng giới hạn bởi đường cong y = √x, trục hoành Ox và đường thẳng x = 4 quanh trục Ox.
Giải:
Thể tích vật thể tròn xoay là:
V = π ∫04 (√x)2 dx = π ∫04 x dx = π [x2/2]04 = π (8) = 8π
Sách giáo khoa Toán 12 Cánh Diều
Các bài giảng trực tuyến về tích phân
Các bài tập luyện tập về ứng dụng hình học của tích phân
Hy vọng với những kiến thức và ví dụ trên, bạn sẽ hiểu rõ hơn về lý thuyết ứng dụng hình học của tích phân Toán 12 Cánh Diều và có thể tự tin giải các bài tập liên quan.