Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 50, 51, 52 sách giáo khoa Toán 12 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Vecto pháp tuyến. Cặp vecto chỉ phương của mặt phẳng
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Cánh diều
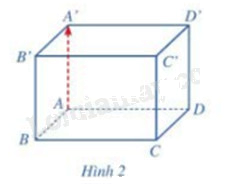
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto \(\overrightarrow {AA'} \) có vuông góc với mặt phẳng (ABCD) hay không?
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Quan sát hình vẽ ta thấy \(\overrightarrow {AA'} \) vuông góc với mặt phẳng (ABCD)
Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Cánh diều
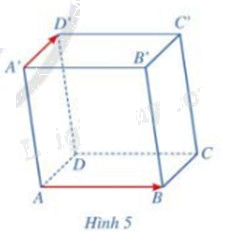
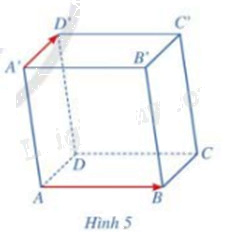
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \)có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)

Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) không cùng phương
Giá của vecto \(\overrightarrow {AB} \) nằm trong mặt phẳng (ABCD)
Giá của vecto \(\overrightarrow {A'D'} \) song song với mặt phẳng (ABCD)
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Cánh diều
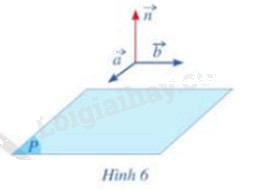
Cho cặp vecto chỉ phương \(\overrightarrow a = (1;0;1),\overrightarrow b = (2;1;0)\) của mặt phẳng (P).
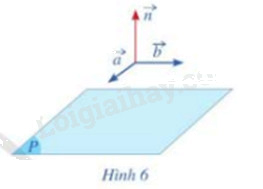
a) Hãy chỉ ra tọa độ của một vecto \(\overrightarrow n (\overrightarrow n \ne \overrightarrow 0 )\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (Hình 6)
b) Vecto \(\overrightarrow n \) có là vecto pháp tuyến của mặt phẳng (P) hay không?
Phương pháp giải:
a) Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)
b) Cho mặt phẳng (P). Nếu vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vecto pháp tuyến của mặt phẳng ()
Lời giải chi tiết:
a) \(\overrightarrow n = (0.0 - 1.1;1.2 - 0.1;1.1 - 2.0) = ( - 1;2;1)\)
b) \(\overrightarrow n \) vuông góc với cả hai vecto chỉ phương của mặt phẳng (P) nên \(\overrightarrow n \) có giá vuông góc với mặt phẳng (P) và là vecto pháp tuyến của mặt phẳng (P)
Trả lời câu hỏi Hoạt động 1 trang 50 SGK Toán 12 Cánh diều
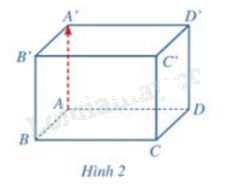
Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vecto \(\overrightarrow {AA'} \) có vuông góc với mặt phẳng (ABCD) hay không?
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Quan sát hình vẽ ta thấy \(\overrightarrow {AA'} \) vuông góc với mặt phẳng (ABCD)
Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Cánh diều
Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \)có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)

Cho hình hộp ABCD.A’B’C’D’. Cho biết hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) và mặt phẳng (ABCD) (Hình 5)
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
Hai vecto \(\overrightarrow {AB} ,\overrightarrow {A'D'} \) không cùng phương
Giá của vecto \(\overrightarrow {AB} \) nằm trong mặt phẳng (ABCD)
Giá của vecto \(\overrightarrow {A'D'} \) song song với mặt phẳng (ABCD)
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Cánh diều
Cho cặp vecto chỉ phương \(\overrightarrow a = (1;0;1),\overrightarrow b = (2;1;0)\) của mặt phẳng (P).
a) Hãy chỉ ra tọa độ của một vecto \(\overrightarrow n (\overrightarrow n \ne \overrightarrow 0 )\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) (Hình 6)
b) Vecto \(\overrightarrow n \) có là vecto pháp tuyến của mặt phẳng (P) hay không?
Phương pháp giải:
a) Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \)
b) Cho mặt phẳng (P). Nếu vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vecto pháp tuyến của mặt phẳng ()
Lời giải chi tiết:
a) \(\overrightarrow n = (0.0 - 1.1;1.2 - 0.1;1.1 - 2.0) = ( - 1;2;1)\)
b) \(\overrightarrow n \) vuông góc với cả hai vecto chỉ phương của mặt phẳng (P) nên \(\overrightarrow n \) có giá vuông góc với mặt phẳng (P) và là vecto pháp tuyến của mặt phẳng (P)
Mục 1 của chương trình Toán 12 tập 2 - Cánh diều tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng, nền tảng cho việc giải quyết nhiều bài toán trong các chương tiếp theo và trong các kỳ thi quan trọng như THPT Quốc gia. Việc nắm vững các khái niệm, định lý và kỹ năng liên quan đến đạo hàm là vô cùng cần thiết.
Bài tập này yêu cầu học sinh vận dụng các quy tắc tính đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp, và đạo hàm của các hàm số lượng giác, hàm mũ, hàm logarit. Để giải bài tập này, học sinh cần xác định đúng hàm số cần tính đạo hàm và áp dụng quy tắc phù hợp.
Bài tập này yêu cầu học sinh tính đạo hàm bậc hai của hàm số, tức là đạo hàm của đạo hàm bậc nhất. Để giải bài tập này, học sinh cần tính đạo hàm bậc nhất trước, sau đó tính đạo hàm của kết quả vừa tìm được.
Bài tập này yêu cầu học sinh sử dụng đạo hàm để tìm cực trị của hàm số, bao gồm cực đại và cực tiểu. Để giải bài tập này, học sinh cần tìm các điểm mà đạo hàm bằng 0 hoặc không tồn tại, sau đó xét dấu của đạo hàm để xác định loại cực trị.
Bài tập này yêu cầu học sinh sử dụng đạo hàm để khảo sát hàm số, bao gồm xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn, và vẽ đồ thị hàm số. Đây là một bài tập tổng hợp, đòi hỏi học sinh phải nắm vững các kiến thức về đạo hàm và kỹ năng phân tích hàm số.
Khi giải các bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 12 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!