Giải bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 2 - Cánh diều. Bài tập 10 trang 64 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và kỹ năng đã được học.

Chúng tôi hiểu rằng việc tự giải bài tập có thể gặp nhiều khó khăn, đặc biệt là đối với những học sinh chưa tự tin về khả năng của mình. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách giải bài tập và áp dụng vào các bài tập tương tự.

Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OBCD có đáy là hình chữ nhật và các điểm O(0;0;0), B(2;0;0), D(0;3;0), S(0;0;4) (hình 19) a) Tìm tọa độ điểm C b) Viết phương trình mặt phẳng (SBD) c) Tính khoảng cách từ điểm C đến mặt phẳng (SBD)

Đề bài

Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OBCD có đáy là hình chữ nhật và các điểm O(0;0;0), B(2;0;0), D(0;3;0), S(0;0;4) (hình 19).

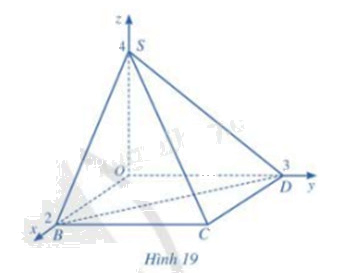
Giải bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều 1

a) Tìm tọa độ điểm C.

b) Viết phương trình mặt phẳng (SBD).

c) Tính khoảng cách từ điểm C đến mặt phẳng (SBD).

Phương pháp giải - Xem chi tiết Giải bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều 2

a) Quan sát hình vẽ.

b) Tìm cặp vecto chỉ phương của mặt phẳng để tìm vecto pháp tuyến. Sử dụng phương trình tổng quát của mặt phẳng.

c) M(a;b;c), (P): Ax + By + Cz + D = 0. Ta có: \(d(M;(P)) = \frac{{\left| {A.a + B.b + C.c + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Lời giải chi tiết

a) C(2;3;0).

b) \(\overrightarrow {SB} = (2;0; - 4);\overrightarrow {SD} = (0;3; - 4)\).

Vecto pháp tuyến của mặt phẳng (SBD) là: \(\overrightarrow n = \left[ {\overrightarrow {SB} ;\overrightarrow {SD} } \right] = (12;8;6) = 2(6;4;3)\).

Phương trình mặt phẳng (SBD) là: \(6x + 4y + 3z - 12 = 0\).

c) \(d(C;(SBD)) = \frac{{\left| {6.2 + 4.3 + 3.0 - 12} \right|}}{{\sqrt {{6^2} + {4^2} + {3^2}} }} = \frac{{12\sqrt {61} }}{{61}}\).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều đặc sắc thuộc chuyên mục đề toán 12 trên nền tảng đề thi toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều: Hướng dẫn chi tiết và dễ hiểu

Bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Phần 1: Tóm tắt lý thuyết cần thiết

Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:

Đạo hàm của hàm số: Đạo hàm của hàm số f(x) tại điểm x, ký hiệu là f'(x), là giới hạn của tỷ số giữa độ biến thiên của hàm số và độ biến thiên của đối số khi độ biến thiên của đối số tiến tới 0.
Quy tắc tính đạo hàm: Có nhiều quy tắc tính đạo hàm khác nhau, như quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp, và các hàm số đặc biệt (hàm lượng giác, hàm mũ, hàm logarit).
Ứng dụng của đạo hàm: Đạo hàm được sử dụng để tìm cực trị của hàm số, khoảng đơn điệu của hàm số, và giải các bài toán tối ưu hóa.

Phần 2: Phân tích bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều

Bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều thường có dạng yêu cầu học sinh tìm đạo hàm của một hàm số hoặc sử dụng đạo hàm để giải quyết một bài toán liên quan đến thực tế. Để giải bài tập này, học sinh cần:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài tập.
Xác định hàm số cần tìm đạo hàm hoặc các thông tin cần thiết để giải bài toán.
Áp dụng các quy tắc tính đạo hàm phù hợp để tìm đạo hàm của hàm số.
Sử dụng đạo hàm để giải quyết bài toán và tìm ra kết quả cuối cùng.

Phần 3: Lời giải chi tiết bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều

(Ở đây sẽ trình bày lời giải chi tiết cho bài tập 10 trang 64, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ, nếu bài tập yêu cầu tìm đạo hàm của hàm số f(x) = x^2 + 2x + 1, lời giải sẽ như sau:)

f'(x) = 2x + 2

Vậy, đạo hàm của hàm số f(x) = x^2 + 2x + 1 là f'(x) = 2x + 2.

Phần 4: Bài tập tương tự và luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo các bài tập tương tự sau:

Tìm đạo hàm của hàm số f(x) = 3x^3 - 2x^2 + x - 5.
Tìm đạo hàm của hàm số f(x) = sin(x) + cos(x).
Tìm đạo hàm của hàm số f(x) = e^x + ln(x).

Phần 5: Kết luận

Bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm vào giải quyết các bài toán thực tế. Hy vọng rằng với hướng dẫn chi tiết và dễ hiểu trên, bạn đã có thể tự giải bài tập này một cách hiệu quả. Chúc bạn học tập tốt!

Lưu ý: Đây chỉ là một ví dụ về cách trình bày lời giải chi tiết cho bài tập 10 trang 64 SGK Toán 12 tập 2 - Cánh diều. Tùy thuộc vào nội dung cụ thể của bài tập, lời giải có thể khác nhau.