Bài 1.1 trang 8 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kiến thức về giới hạn của hàm số. Bài tập này yêu cầu học sinh phải nắm vững định nghĩa, tính chất của giới hạn và các phương pháp tính giới hạn cơ bản.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.1 trang 8 sách bài tập Toán 12 Kết nối tri thức, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
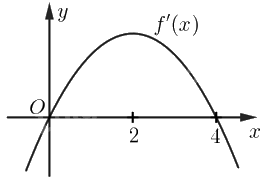
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết: a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\); b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Đề bài
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết:
a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\);
b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Phương pháp giải - Xem chi tiết
Ý a: Quan sát đồ thị để xác định dấu của đạo hàm, từ đó biết được các khoảng đồng biến, nghịch biến của hàm số.
Ý b: Xác định các điểm trên đồ thị mà tại đó đạo hàm đổi dấu, đó chính là các điểm cực trị của hàm số.
Lời giải chi tiết
a) Từ đồ thị ta có:
\(f'\left( x \right) > 0{\rm{ }}\forall {\rm{x}} \in \left( {0;4} \right)\) nên hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;4} \right)\).
\(f'\left( x \right) < 0{\rm{ }}\)với mọi \({\rm{x}}\) thuộc \(\left( { - \infty ;0} \right)\) và \({\rm{x}}\) thuộc \(\left( {4; + \infty } \right)\) nên hàm số \(f\left( x \right)\) nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {4; + \infty } \right)\).
b) Ta có hàm số \(f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Vì \(f'\left( x \right)\) đổi dấu từ âm sang dương khi \(x\) đi qua \(0\) nên hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = 0\); \(f'\left( x \right)\) đổi dấu từ dương sang âm khi \(x\) đi qua \(4\) nên hàm số \(f\left( x \right)\) đạt cực đại tại \(x = 4\)
Bài 1.1 trang 8 sách bài tập Toán 12 Kết nối tri thức yêu cầu tính giới hạn của hàm số. Để giải bài này, chúng ta cần nắm vững các khái niệm cơ bản về giới hạn, bao gồm định nghĩa, các tính chất và các phương pháp tính giới hạn.
Tính các giới hạn sau:
Để giải các bài toán về giới hạn, chúng ta có thể sử dụng các phương pháp sau:
a) limx→2 (x2 - 4) / (x - 2)
Ta có thể phân tích thành nhân tử biểu thức x2 - 4 thành (x - 2)(x + 2). Do đó:
limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
b) limx→3 (x3 - 27) / (x - 3)
Ta có thể phân tích thành nhân tử biểu thức x3 - 27 thành (x - 3)(x2 + 3x + 9). Do đó:
limx→3 (x3 - 27) / (x - 3) = limx→3 (x - 3)(x2 + 3x + 9) / (x - 3) = limx→3 (x2 + 3x + 9) = 32 + 3*3 + 9 = 9 + 9 + 9 = 27
c) limx→0 sin(x) / x
Đây là một giới hạn đặc biệt, ta có thể sử dụng công thức giới hạn đặc biệt:
limx→0 sin(x) / x = 1
Vậy, kết quả của các giới hạn là:
Để hiểu rõ hơn về giới hạn, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng giải bài tập.
Việc nắm vững kiến thức về giới hạn là rất quan trọng để học tốt các chương trình toán học cao hơn. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt được kết quả tốt nhất.