Bài 1.31 trang 25 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.31 trang 25 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hãy cùng theo dõi lời giải chi tiết dưới đây!
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) (y = {x^3} - 6{x^2} + 9x); b) (y = {x^3} + 3{x^2} + 6x + 4).
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = {x^3} - 6{x^2} + 9x\);
b) \(y = {x^3} + 3{x^2} + 6x + 4\).
Phương pháp giải - Xem chi tiết
+ Tìm tập xác định của hàm số
+ Khảo sát sự biến thiên của hàm số: Tính đạo hàm, tìm các khoảng đồng biến, nghịch biến của đồ thị, tìm các điểm cực trị, cực trị, giới hạn tại vô cực, ghi kết quả tìm được vào bảng biến thiên.
+ Vẽ đồ thị dựa vào bảng biến thiên, khi vẽ lưu ý đến tính đối xứng, tọa độ giao điểm với các trục.
+ Chú ý: đồ thị hàm số bậc ba có tâm đối xứng là điểm có hoàng độ thỏa mãn \(y'' = 0\).
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\).
Sự biến thiên:
+ Ta có \(y' = 3{x^2} - 12x + 9\). Khi đó \(y' = 0 \Leftrightarrow 3{x^2} - 12x + 9 = 0 \Leftrightarrow x = 1\) hoặc \(x = 3\).
+ Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right)\), nghịch biến trên khoảng \(\left( {1;3} \right)\).
+ Hàm số đạt cực đại tại \(x = 1\) với \({y_{CĐ}} = 4\), đạt cực tiểu tại \(x = 3\) với \({y_{CT}} = 0\).
+ Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } = + \infty \).
+ Bảng biến thiên:
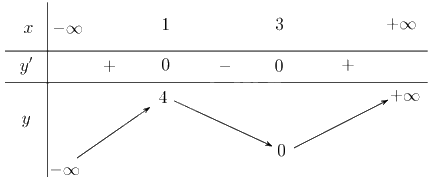
Đồ thị: Đồ thị của hàm số cắt trục tung tại điểm \(\left( {0;0} \right)\), cắt trục hoành tại hai điểm \(\left( {0;0} \right)\) và \(\left( {3;0} \right)\). Đồ thị nhận \(\left( {2;2} \right)\) làm tâm đối xứng.
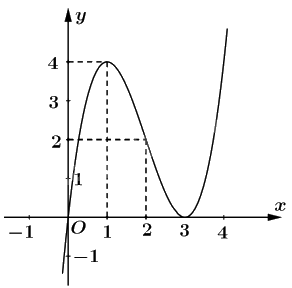
b) Tập xác định: \(\mathbb{R}\).
Sự biến thiên:
+ Ta có \(y' = 3{x^2} + 6x + 6 > 0\) với mọi \(x\).
+ Hàm số đồng biến trên \(\mathbb{R}\).
+ Hàm số không có cực trị.
+ Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty \), \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \).
+ Bảng biến thiên:
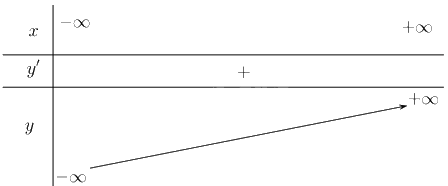
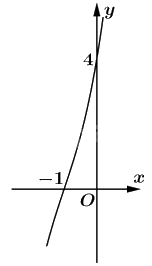
Đồ thị: Đồ thị của hàm số cắt trục tung tại điểm \(\left( {0;4} \right)\), cắt trục hoành tại điểm \(\left( { - 1;0} \right)\), đồ thị có tâm đối xứng là điểm \(\left( { - 1;0} \right)\).
Bài 1.31 trang 25 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 1.31 thường yêu cầu học sinh giải quyết các bài toán liên quan đến việc tìm đạo hàm của hàm số, xác định các điểm cực trị, và khảo sát sự biến thiên của hàm số. Cụ thể, bài tập có thể yêu cầu:
Để giải bài 1.31 trang 25 Sách bài tập Toán 12 - Kết nối tri thức, học sinh có thể thực hiện theo các bước sau:
Giả sử bài 1.31 yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x.
Giải:
f'(x) = 3x2 - 6x + 2
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x + 2 = 0
Giải phương trình bậc hai này, ta được hai nghiệm x1 và x2. Đây là các điểm cực trị của hàm số.
Để xác định khoảng đồng biến, nghịch biến, ta xét dấu f'(x) trên các khoảng (-∞, x1), (x1, x2), và (x2, +∞).
Ngoài sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau để học tập hiệu quả:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn giải bài 1.31 trang 25 Sách bài tập Toán 12 - Kết nối tri thức trên đây, các em học sinh sẽ hiểu rõ hơn về kiến thức đạo hàm và tự tin làm bài tập. Chúc các em học tập tốt!