Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 1.66 trang 36, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi cam kết cung cấp nội dung chính xác, cập nhật và phù hợp với chương trình học Toán 12 hiện hành. Hãy cùng bắt đầu với lời giải chi tiết của bài tập này.
Cho hàm số (y = frac{{m{x^2} + left( {2m - 1} right)x - 1}}{{x + 2}}) với (m) là tham số. a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi (m > 0). b) Khảo sát và vẽ đồ thị (left( H right)) của hàm số đã cho với (m = 1). c) Giả sử (Delta ) là tiếp tuyến của đồ thị (left( H right)) tại điểm (M in left( H right)) bất kì. Chứng minh rằng nếu (Delta ) cắt tiệm cận đứng và tiệm cận xiên của (left( H right)) tại A và B thì M luôn là trung điểm của
Đề bài
Cho hàm số \(y = \frac{{m{x^2} + \left( {2m - 1} \right)x - 1}}{{x + 2}}\) với \(m\) là tham số.
a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi \(m > 0\).
b) Khảo sát và vẽ đồ thị \(\left( H \right)\) của hàm số đã cho với \(m = 1\).
c) Giả sử \(\Delta \) là tiếp tuyến của đồ thị \(\left( H \right)\) tại điểm \(M \in \left( H \right)\) bất kì. Chứng minh rằng nếu \(\Delta \) cắt tiệm cận đứng và tiệm cận xiên của \(\left( H \right)\) tại A và B thì M luôn là trung điểm của đoạn AB.
Phương pháp giải - Xem chi tiết
Ý a: Xét dấu đạo hàm và lập bảng biến thiên.
Ý b: Khảo sát và vẽ đồ thị hàm số \(\left( H \right)\).
Ý c: Giả sử điểm M thuộc đồ thị biểu diễn tọa độ theo một tham số, từ đó viết phương trình tiếp tuyến tại M của đồ thị phụ thuộc tham số sau đó giải để tìm được tọa độ A và B theo tham số, từ đó tính toán tọa độ trung điểm sẽ suy ra điều phải chứng minh.
Lời giải chi tiết
a) Ta có \(y' = \frac{{\left( {2mx + 2m - 1} \right)\left( {x + 2} \right) + m{x^2} + \left( {2m - 1} \right)x - 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{m{x^2} + 4mx + 4m - 1}}{{{{\left( {x + 2} \right)}^2}}}\).
Khi đó \(y' = 0 \Leftrightarrow m{x^2} + 4mx + 4m - 1 = 0{\rm{ }}\left( {x \ne - 2} \right)\).
Xét phương trình \(m{x^2} + 4mx + 4m - 1 = 0{\rm{ }}\)
Ta có \(\Delta ' = {\left( {2m} \right)^2} - 4{m^2} + m = m\). Do đó nếu \(m > 0\) thì phương trình luôn có hai nghiệm phân biệt: \({x_1} = \frac{{ - 2m - \sqrt m }}{m} = - 2 - \frac{1}{{\sqrt m }}\); \({x_2} = \frac{{ - 2m + \sqrt m }}{m} = - 2 + \frac{1}{{\sqrt m }}\).
Lập bảng biến thiên:
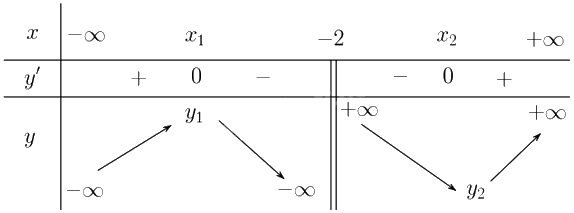
Từ bảng biến thiên suy ra hàm số luôn có tiểu và cực đại với mọi \(m > 0\).
b) Với \(m = 1\) ta có \(\left( H \right):{\rm{ }}y = \frac{{{x^2} + x - 1}}{{x + 2}}\).
Tập xác định: \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có \(y' = \frac{{\left( {2x + 1} \right)\left( {x + 2} \right) - {x^2} - x + 1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
Suy ra \(y' = 0 \Leftrightarrow \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}} = 0 \Leftrightarrow {x^2} + 4x + 3 = 0 \Leftrightarrow x = - 3\) hoặc \(x = - 1\).
Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty \).
\(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{{x^2} + x - 1}}{{x + 2}} = + \infty \) và \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} + x - 1}}{{x + 2}} = - \infty \) suy ra \(x = - 2\) là tiệm cận đứng.
Ta có \(y = \frac{{{x^2} + x - 1}}{{x + 2}} = x - 1 + \frac{1}{{x + 2}}\); \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \frac{1}{{x + 2}} = 0\) suy ra \(y = x - 1\) là tiệm cận xiên
Ta lập bảng biến thiên
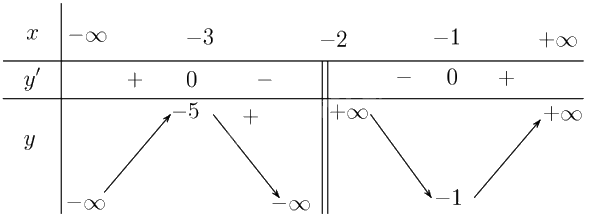
Đồ thị:
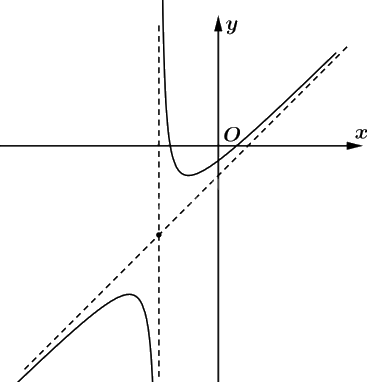
c) Giả sử \(M \in \left( H \right)\) bất kì suy ra \(M\left( {t;\frac{{{t^2} + t - 1}}{{t + 2}}} \right)\).
Tiếp tuyến của \(\left( H \right)\) tại \(M\) có phương trình là
\(\Delta :y = y'\left( t \right)\left( {x - t} \right) + \frac{{{t^2} + t - 1}}{{t + 2}} \Leftrightarrow y = \frac{{{t^2} + 4t + 3}}{{{{\left( {t + 2} \right)}^2}}}\left( {x - t} \right) + \frac{{{t^2} + t - 1}}{{t + 2}}\).
Tiếp tuyến cắt tiệm cận đứng \(x = - 2\) tại \(A\left( { - 2; - \frac{{3t + 4}}{{t + 2}}} \right)\), cắt tiệm cận xiên \(y = x - 1\) tại
\(B\left( {2t + 2;2t + 1} \right)\). Khi đó ta có \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2t = 2{x_M}\\{y_A} + {y_B} = \left( {2t + 1} \right) - \frac{{3t + 4}}{{t + 2}} = \frac{{2{t^2} + 2t - 2}}{{t + 2}} = 2{y_M}\end{array} \right.\).
Vậy M là trung điểm của đoạn AB.
Bài 1.66 trang 36 sách bài tập Toán 12 Kết nối tri thức yêu cầu giải một bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, cực trị của hàm số và các bước giải bài toán khảo sát hàm số.
Trước khi bắt đầu giải bài, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 1.66, yêu cầu thường là tìm cực trị, khoảng đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số hoặc giải các bài toán liên quan đến ứng dụng của đạo hàm trong thực tế.
Giả sử bài 1.66 yêu cầu khảo sát hàm số f(x) = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước trên để giải bài toán này.
| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| f'(x) | + | - | + |
| Khoảng | x < 1 | x > 1 |
|---|---|---|
| f''(x) | - | + |
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài 1.66 trang 36 sách bài tập Toán 12 Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!