Bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này thường yêu cầu học sinh phải vận dụng các định nghĩa và tính chất của giới hạn để tìm ra kết quả chính xác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau: a) (y = x + frac{1}{x}); b) (y = frac{x}{{{x^2} + 1}}).
Đề bài
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:
a) \(y = x + \frac{1}{x}\);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Phương pháp giải - Xem chi tiết
Ý a:
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\) hoặc đạo hàm không tồn tại.
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Ý b:
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\backslash \left\{ 0 \right\}\)
Ta có \(y' = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\). Khi đó \(y' = 0 \Leftrightarrow \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
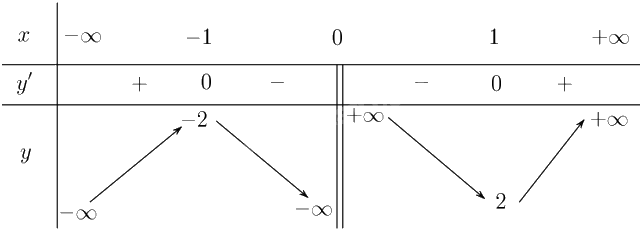
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Hàm số đạt cực đại tại \(x = - 1\) và \({y_{CĐ}} = y\left( -1 \right) = -2\).
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 2\).
b) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = \frac{{1 \cdot \left( {{x^2} + 1} \right) - x \cdot 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} = \frac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}\).
Khi đó \(y' = 0 \Leftrightarrow \frac{{ - {x^2} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0 \Leftrightarrow - {x^2} + 1 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
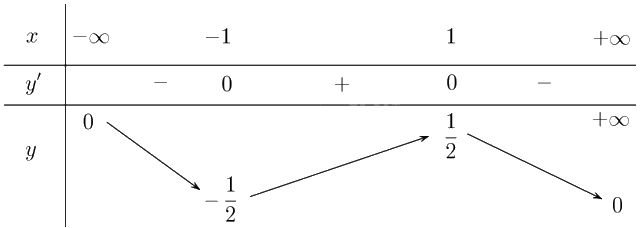
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đạt cực đại tại \(x = 1\) và \({y_{CĐ}} = y\left( { - 1} \right) = \frac{1}{2}\).
Hàm số đạt cực tiểu tại \(x = - 1\) và \({y_{CT}} = y\left( { - 1} \right) = - \frac{1}{2}\).
Bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức thuộc chương 1: Giới hạn. Chủ đề chính của bài tập này là giới hạn của hàm số tại một điểm và giới hạn vô cùng. Việc nắm vững kiến thức về giới hạn là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Bài tập 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức thường bao gồm các dạng bài sau:
Để giải bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức, chúng ta cần thực hiện các bước sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 1.3 trang 9:
Giả sử hàm số f(x) = (x^2 - 1) / (x - 1). Hãy tính giới hạn của f(x) khi x tiến tới 1.
Lời giải:
Ta có thể phân tích f(x) như sau: f(x) = (x - 1)(x + 1) / (x - 1) = x + 1 (với x ≠ 1). Do đó, lim (x→1) f(x) = lim (x→1) (x + 1) = 1 + 1 = 2.
Giả sử hàm số g(x) = (x^3 - 8) / (x - 2). Hãy tính giới hạn của g(x) khi x tiến tới 2.
Lời giải:
Ta có thể phân tích g(x) như sau: g(x) = (x - 2)(x^2 + 2x + 4) / (x - 2) = x^2 + 2x + 4 (với x ≠ 2). Do đó, lim (x→2) g(x) = lim (x→2) (x^2 + 2x + 4) = 2^2 + 2*2 + 4 = 12.
Giả sử hàm số h(x) = 1 / x. Hãy tính giới hạn của h(x) khi x tiến tới vô cùng.
Lời giải:
Khi x tiến tới vô cùng, 1/x tiến tới 0. Do đó, lim (x→∞) h(x) = 0.
Giới hạn có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 1.3 trang 9 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức về giới hạn. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự.