Bài 3.22 trang 69 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.22 trang 69 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một người đầu tư cùng một số tiền vào hai lĩnh vực A và B. Nhà đầu tư này ghi lại số tiền thu được hằng tháng trong hai năm theo mỗi lĩnh vực cho kết quả như sau: Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và nhận xét về mức độ ổn định của số tiền thu được hằng tháng khi đầu tư vào hai lĩnh vực trên.
Đề bài
Một người đầu tư cùng một số tiền vào hai lĩnh vực A và B. Nhà đầu tư này ghi lại số tiền thu được hằng tháng trong hai năm theo mỗi lĩnh vực cho kết quả như sau:
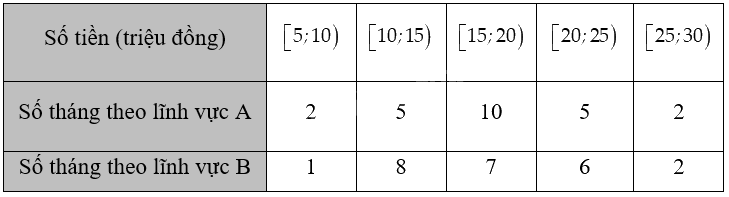
Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và nhận xét về mức độ ổn định của số tiền thu được hằng tháng khi đầu tư vào hai lĩnh vực trên.
Phương pháp giải - Xem chi tiết
Xét từng mẫu số liệu ghép nhóm, sử dụng các công thức đã học để tìm số trung bình và độ lệch chuẩn của chúng. So sánh hai giá trị độ lệch chuẩn để rút ra nhận xét về mức độ ổn định của số tiền thu được hằng tháng khi đầu tư vào hai lĩnh vực.
Lời giải chi tiết
+ Xét mẫu số liệu về số tiền thu được hằng tháng trong hai năm theo lĩnh vực A:
Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:

Cỡ mẫu là \(n = 24\).
Giá trị trung bình của mẫu số liệu là
\(\overline {{x_A}} = \frac{{7,5 \cdot 2 + 12,5 \cdot 5 + 17,5 \cdot 10 + 22,5 \cdot 5 + 27,5 \cdot 2}}{{24}} = \frac{{420}}{{24}} = 17,5\).
Độ lệch chuẩn của mẫu số liệu là
\(\begin{array}{l}{s_A} = \sqrt {\frac{1}{n}\left( {{{7,5}^2} \cdot 2 + {{12,5}^2} \cdot 5 + {{17,5}^2} \cdot 10 + {{22,5}^2} \cdot 5 + {{27,5}^2} \cdot 2} \right) - {{\left( {\overline {{x_A}} } \right)}^2}} \\{\rm{ }} = \sqrt {\frac{{8000}}{{24}} - {{17,5}^2}} = \sqrt {\frac{{325}}{{12}}} \approx 5,2042.\end{array}\)
+ Xét mẫu số liệu về số tiền thu được hằng tháng trong hai năm theo lĩnh vực A:
Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:

Cỡ mẫu là \(m = 24\).
Giá trị trung bình của mẫu số liệu là
\(\overline {{x_B}} = \frac{{7,5 \cdot 1 + 12,5 \cdot 8 + 17,5 \cdot 7 + 22,5 \cdot 6 + 27,5 \cdot 2}}{{24}} = \frac{{420}}{{24}} = 17,5\).
Độ lệch chuẩn của mẫu số liệu là
\(\begin{array}{l}{s_B} = \sqrt {\frac{1}{m}\left( {{{7,5}^2} \cdot 1 + {{12,5}^2} \cdot 8 + {{17,5}^2} \cdot 7 + {{22,5}^2} \cdot 6 + {{27,5}^2} \cdot 2} \right) - {{\left( {\overline {{x_B}} } \right)}^2}} \\{\rm{ }} = \sqrt {\frac{{8000}}{{24}} - {{17,5}^2}} = \sqrt {\frac{{325}}{{12}}} \approx 5,2042.\end{array}\)
Ta có \({x_A} = {x_B}\) và \({s_A} = {s_B}\). Suy ra giá trị trung bình và độ lệch chuẩn của hai mẫu số liệu giống nhau. Do độ lệch chuẩn bằng nhau nên mức độ ổn định của hai phương án đầu tư là như nhau.
Bài 3.22 trang 69 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập 3.22:
Bài tập yêu cầu tính đạo hàm của hàm số tại một điểm cho trước hoặc tìm điều kiện để hàm số có đạo hàm tại một điểm. Thông thường, bài tập sẽ cho một hàm số cụ thể và yêu cầu tính đạo hàm f'(x) hoặc f'(x0).
Hướng dẫn giải bài 3.22:
Ví dụ minh họa:
Giả sử hàm số cần tính đạo hàm là f(x) = x2 + 2x + 1. Để tính đạo hàm f'(x), ta áp dụng quy tắc đạo hàm của hàm số đa thức:
f'(x) = 2x + 2
Các dạng bài tập thường gặp:
Lưu ý khi giải bài tập:
Tài liệu tham khảo:
Kết luận:
Bài 3.22 trang 69 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc tính đạo hàm và áp dụng chúng một cách linh hoạt, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc học Toán 12.
Để hiểu rõ hơn về các khái niệm và phương pháp giải bài tập về đạo hàm, các bạn có thể tham khảo thêm các bài viết và video hướng dẫn trên giaitoan.edu.vn. Chúc các bạn học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |