Bài 4.21 trang 17 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.21 trang 17 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Tính diện tích của các hình phẳng được tô màu dưới đây:
Đề bài
Tính diện tích của các hình phẳng được tô màu dưới đây:
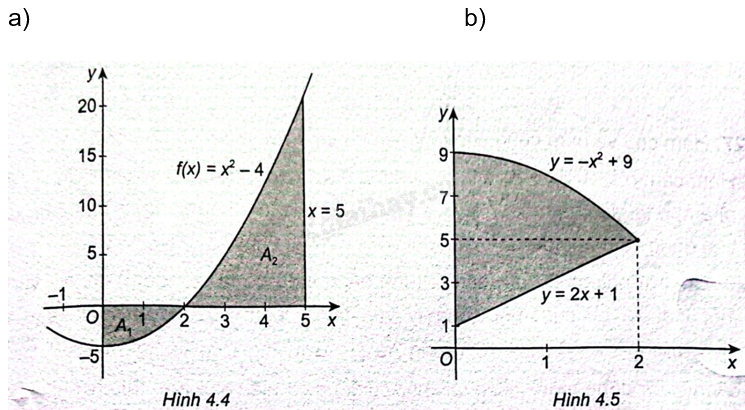
Phương pháp giải - Xem chi tiết
Ý a: Xác định xem hình vẽ được giới hạn bởi các đường nào sau đó sử dụng công thức tính diện tích bằng tích phân.
Ý b: Xác định xem hình vẽ được giới hạn bởi các đường nào sau đó sử dụng công thức tính diện tích bằng tích phân.
Lời giải chi tiết
a) Hình phẳng được giới hạn bởi các đường \(y = f\left( x \right),x = 0\) và \(x = 5\).
Diện tích cần tìm là \(S = \int\limits_0^5 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^5 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left( { - {x^2} + 4} \right)dx} + \int\limits_2^5 {\left( {{x^2} - 4} \right)dx} \)
\( = \left. {\left( {\frac{{ - {x^3}}}{3} + 4x} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - 4x} \right)} \right|_2^5 = \frac{{ - 8}}{3} + 8 + \frac{{125}}{3} - 20 - \frac{8}{3} + 8 = \frac{{97}}{3}\).
b) Hình phẳng cần tìm được giới hạn bởi các đường \(y = - {x^2} + 9,{\rm{ }}y = 2x + 1,{\rm{ }}x = 0\) và \(x = 2\).
Diện tích cần tìm là
\(S = \int\limits_0^2 {\left| {\left( { - {x^2} + 9} \right) - \left( {2x + 1} \right)} \right|dx} = \int\limits_0^2 {\left[ {\left( { - {x^2} + 9} \right) - \left( {2x + 1} \right)} \right]dx} = \int\limits_0^2 {\left( { - {x^2} + 9 - 2x - 1} \right)dx} \)
\( = \int\limits_0^2 {\left( { - {x^2} - 2x + 8} \right)dx} = \left. {\left( { - \frac{{{x^3}}}{3} - {x^2} + 8x} \right)} \right|_0^2 = - \frac{8}{3} - 4 + 16 = \frac{{28}}{3}\).
Bài 4.21 trang 17 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 4.21 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu chúng ta tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1.
Bước 1: Tính đạo hàm f'(x)
Áp dụng quy tắc tính đạo hàm của hàm số đa thức, ta có:
f'(x) = 3x2 - 6x + 2
Bước 2: Tìm điểm cực trị
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x + 2 = 0
Sử dụng công thức nghiệm của phương trình bậc hai, ta tìm được hai nghiệm:
x1 = (6 + √12) / 6 = 1 + √3 / 3
x2 = (6 - √12) / 6 = 1 - √3 / 3
Bước 3: Xác định loại điểm cực trị
Để xác định loại điểm cực trị, ta xét dấu của đạo hàm bậc hai f''(x):
f''(x) = 6x - 6
Tại x1 = 1 + √3 / 3, f''(x1) = 6(1 + √3 / 3) - 6 = 2√3 > 0, do đó x1 là điểm cực tiểu.
Tại x2 = 1 - √3 / 3, f''(x2) = 6(1 - √3 / 3) - 6 = -2√3 < 0, do đó x2 là điểm cực đại.
Khi giải bài tập về đạo hàm, các em học sinh cần lưu ý những điều sau:
Giaitoan.edu.vn là website học Toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi hy vọng rằng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin hơn khi giải bài tập 4.21 trang 17 Sách bài tập Toán 12 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin x | y' = cos x |
| y = cos x | y' = -sin x |