Bài 2.8 trang 45 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
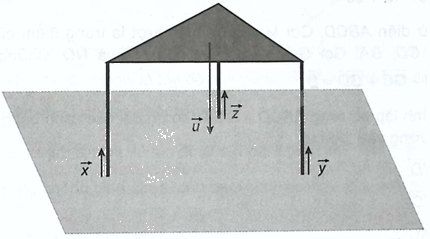
Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và ba chân bàn vuông góc với mặt sàn. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ (overrightarrow u )) phân tán đều qua các chân bàn và tạo nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ (overrightarrow x ,{rm{ }}overrightarrow y ,{rm{ }}overrightarrow z )). Hãy giải thích vì sao (overrightarrow x = overrightarrow y = overrightarrow z = - frac{1}{3}overrightarrow u )
Đề bài
Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và ba chân bàn vuông góc với mặt sàn. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ \(\overrightarrow u \)) phân tán đều qua các chân bàn và tạo nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ \(\overrightarrow x ,{\rm{ }}\overrightarrow y ,{\rm{ }}\overrightarrow z \)). Hãy giải thích vì sao \(\overrightarrow x = \overrightarrow y = \overrightarrow z = - \frac{1}{3}\overrightarrow u \).
Phương pháp giải - Xem chi tiết
Từ từng ý trong đề bài suy ra được hướng, phương, độ lớn của \(\overrightarrow x ,{\rm{ }}\overrightarrow y ,{\rm{ }}\overrightarrow z \) và mối liên hệ của chúng với trọng lực.
Lời giải chi tiết
Các vectơ \(\overrightarrow x ,{\rm{ }}\overrightarrow y ,{\rm{ }}\overrightarrow z \) đôi một cùng phương vì đều có giá vuông góc với mặt đất, cùng hướng vì chúng ngược hướng với trọng lực và chúng có độ lớn bằng nhau vì trọng lực phân tán đều qua ba chân bàn.
Do đó \(\overrightarrow x = \overrightarrow y = \overrightarrow z \) và \(\left| {\overrightarrow x } \right| = \left| {\overrightarrow y } \right| = \left| {\overrightarrow z } \right| = \frac{1}{3}\left| {\overrightarrow u } \right|\).
Vậy \(\overrightarrow x = \overrightarrow y = \overrightarrow z = - \frac{1}{3}\overrightarrow u \).
Bài 2.8 trang 45 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập:
Bài 2.8 yêu cầu học sinh tính đạo hàm của hàm số tại một điểm cho trước hoặc tìm điều kiện để hàm số có đạo hàm. Bài tập thường được trình bày dưới dạng các hàm số phức tạp, đòi hỏi học sinh phải phân tích và áp dụng linh hoạt các quy tắc tính đạo hàm.
Để giải bài 2.8 trang 45, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tính đạo hàm là f(x) = x2 + 2x + 1. Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của hàm đa thức:
f'(x) = 2x + 2
Vậy, đạo hàm của hàm số f(x) = x2 + 2x + 1 là f'(x) = 2x + 2.
Ngoài bài 2.8, còn rất nhiều bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức. Các bài tập này thường yêu cầu học sinh:
Để nắm vững kiến thức về đạo hàm, học sinh cần luyện tập thường xuyên và hiểu rõ các quy tắc tính đạo hàm. Ngoài ra, việc tham khảo các tài liệu học tập khác và tìm kiếm sự giúp đỡ từ giáo viên cũng rất quan trọng.
Dưới đây là một số mẹo giúp bạn giải bài tập đạo hàm hiệu quả:
Bảng tổng hợp các quy tắc đạo hàm cơ bản:
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin giải bài 2.8 trang 45 Sách bài tập Toán 12 - Kết nối tri thức và các bài tập tương tự. Chúc các bạn học tốt!