Bài 1.11 trang 14 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Sử dụng đồ thị dưới đây, xác định xem hàm số (y = fleft( x right)) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm ({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}) hay không.
Đề bài
Sử dụng đồ thị dưới đây, xác định xem hàm số \(y = f\left( x \right)\) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}\) hay không.
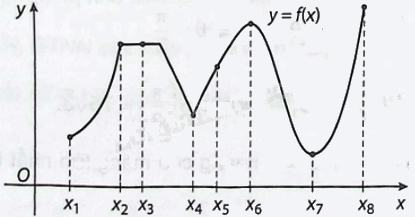
Phương pháp giải - Xem chi tiết
Quan sát đồ thị kết hợp với định nghĩa cực trị, giá trị lớn nhất, nhỏ nhất của hàm số để đưa ra kết luận.
Lời giải chi tiết
Ta có hàm số \(y = f\left( x \right)\) xác định trên \(\left[ {{x_1};{x_8}} \right]\). Từ đồ thị ta có:
+ \(f\left( x \right) \le f\left( {{x_8}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_8} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_8}} \right)\). Do đó hàm số đạt giá trị lớn nhất tại điểm \({x_8}\).
+ \(f\left( x \right) \ge f\left( {{x_7}} \right)\) với mọi \(x \in \left[ {{x_1};{x_8}} \right]\) và \({x_7} \in \left[ {{x_1};{x_8}} \right]\) thỏa mãn \(f\left( x \right) = f\left( {{x_7}} \right)\). Do đó hàm số
đạt giá trị nhỏ nhất tại điểm \({x_7}\).
Ta có hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ {{x_1};{x_8}} \right]\).
+ Gọi \({h_1} = \frac{{{x_5} - {x_4}}}{2}\) , ta thấy \({h_1}\) dương. Vì \(f\left( x \right) > f\left( {{x_4}} \right)\) với mọi \(x \in \left( {{x_4} - {h_1};{x_4} + {h_1}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_4}\) nên hàm số đạt cực tiểu tại điểm \({x_4}\).
+ Tương tự, gọi \({h_2} = \frac{{{x_8} - {x_7}}}{2}\) , ta thấy \({h_2}\) dương. Vì \(f\left( x \right) > f\left( {{x_7}} \right)\) với mọi \(x \in \left( {{x_7} - {h_2};{x_7} + {h_2}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_7}\) nên hàm số đạt cực tiểu tại điểm \({x_7}\).
+ Gọi \({h_3} = \frac{{{x_6} - {x_5}}}{2}\) , ta thấy \({h_3}\) dương. Vì \(f\left( x \right) < f\left( {{x_6}} \right)\) với mọi \(x \in \left( {{x_6} - {h_3};{x_6} + {h_3}} \right) \subset \left[ {{x_1};{x_8}} \right]\) và \(x \ne {x_6}\) nên hàm số đạt cực đại tại điểm \({x_6}\).
Bài 1.11 trang 14 sách bài tập Toán 12 - Kết nối tri thức yêu cầu học sinh tính giới hạn của hàm số. Để giải bài tập này, chúng ta cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, đặc biệt là giới hạn của các hàm số đơn giản như hàm đa thức, hàm phân thức.
Đề bài thường yêu cầu tính giới hạn của một hàm số khi x tiến tới một giá trị cụ thể. Việc xác định đúng phương pháp giải là rất quan trọng. Các phương pháp thường được sử dụng bao gồm:
(Nội dung lời giải chi tiết bài 1.11 trang 14 sẽ được trình bày tại đây. Bao gồm các bước giải cụ thể, giải thích rõ ràng từng bước và kết quả cuối cùng. Ví dụ:)
Ví dụ: Tính limx→2 (x2 - 4) / (x - 2)
Ngoài bài 1.11, sách bài tập Toán 12 - Kết nối tri thức còn nhiều bài tập tương tự về giới hạn hàm số. Để giải tốt các bài tập này, các em cần:
Giới hạn hàm số là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 1.11 trang 14 sách bài tập Toán 12 - Kết nối tri thức là một bài tập cơ bản về giới hạn hàm số. Việc nắm vững kiến thức và luyện tập thường xuyên sẽ giúp các em học sinh giải quyết bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ học tập tốt hơn môn Toán 12.
| Khái niệm | Giải thích |
|---|---|
| Giới hạn hàm số | Giá trị mà hàm số tiến tới khi x tiến tới một giá trị cụ thể. |
| Giới hạn một bên | Giới hạn của hàm số khi x tiến tới một giá trị từ bên trái hoặc bên phải. |