Bài 1.18 trang 15 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.18 trang 15 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hai nguồn nhiệt đặt cách nhau \(s\) mét, một nguồn có cường độ \(a\) đặt ở điểm A và một nguồn có cường độ \(b\) đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức \(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},\) Trong đó \(x\) (m) là khoảng cách giữa P và A. Tại điểm nào giữa A và B, nhiệt độ sẽ thấp nhất?
Đề bài
Hai nguồn nhiệt đặt cách nhau \(s\) mét, một nguồn có cường độ \(a\) đặt ở điểm A và một nguồn có cường độ \(b\) đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức
\(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},\)
Trong đó \(x\) (m) là khoảng cách giữa P và A. Tại điểm nào giữa A và B, nhiệt độ sẽ thấp nhất?
Phương pháp giải - Xem chi tiết
Xét hàm số \(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},{\rm{ }}0 \le x \le s\). Yêu cầu bài toán tương đương tìm \(x\) để hàm số đạt giá trị nhỏ nhất. Tính đạo hàm, lập bảng biến thiên của hàm số và đưa ra kết luận.
Lời giải chi tiết
Xét hàm số \(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},{\rm{ }}0 \le x \le s\). Ta cần tìm \(x\) để hàm số đạt giá trị nhỏ nhất.
Ta có: \(I' = - \frac{{2a}}{{{x^3}}} + \frac{{2b}}{{{{\left( {s - x} \right)}^3}}} = \frac{{2\left[ {b{x^3} - a{{\left( {s - x} \right)}^3}} \right]}}{{{x^3}{{\left( {s - x} \right)}^3}}},{\rm{ }}0 \le x \le s\)
Khi đó \(I' = 0 \Leftrightarrow \frac{{2\left[ {b{x^3} - a{{\left( {s - x} \right)}^3}} \right]}}{{{x^3}{{\left( {s - x} \right)}^3}}} = 0 \Leftrightarrow 2\left[ {b{x^3} - a{{\left( {s - x} \right)}^3}} \right] = 0 \Leftrightarrow \frac{x}{{s - x}} = \frac{{\sqrt[3]{a}}}{{\sqrt[3]{b}}} \Leftrightarrow x = \frac{{s\sqrt[3]{a}}}{{\sqrt[3]{a} + \sqrt[3]{b}}}\).
Lập bảng biến thiên của hàm số:
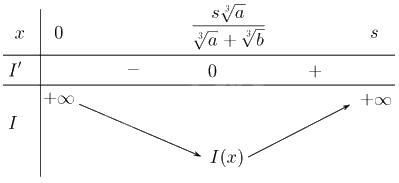
Từ bảng biến thiên suy ra hàm số đạt giá trị nhỏ nhất tại \(x = \frac{{s\sqrt[3]{a}}}{{\sqrt[3]{a} + \sqrt[3]{b}}}\).
Vậy tại điểm P trên đoạn AB các A một khoảng \(PA = x = \frac{{s\sqrt[3]{a}}}{{\sqrt[3]{a} + \sqrt[3]{b}}}\)(m) thì nhiệt độ thấp nhất.
Bài 1.18 trang 15 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Bài tập yêu cầu tính các giới hạn sau:
lim (x→2) (x^2 - 4) / (x - 2)
lim (x→3) (x^3 - 27) / (x - 3)
lim (x→0) sin(x) / x
Để giải bài tập này, chúng ta có thể sử dụng các phương pháp sau:
Phân tích thành nhân tử: Đối với các biểu thức chứa đa thức, ta có thể phân tích thành nhân tử để rút gọn biểu thức và tính giới hạn.
Sử dụng công thức giới hạn đặc biệt: Một số giới hạn đặc biệt như lim (sin(x) / x) khi x→0 có công thức giới hạn đã được biết đến.
Áp dụng các tính chất của giới hạn: Sử dụng các tính chất của giới hạn như giới hạn của tổng, hiệu, tích, thương để tính giới hạn của biểu thức phức tạp.
Ta có thể phân tích x^2 - 4 thành (x - 2)(x + 2). Do đó:
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
Ta có thể phân tích x^3 - 27 thành (x - 3)(x^2 + 3x + 9). Do đó:
lim (x→3) (x^3 - 27) / (x - 3) = lim (x→3) (x - 3)(x^2 + 3x + 9) / (x - 3) = lim (x→3) (x^2 + 3x + 9) = 3^2 + 3*3 + 9 = 9 + 9 + 9 = 27
Đây là một giới hạn đặc biệt. Ta có:
lim (x→0) sin(x) / x = 1
Luôn kiểm tra xem biểu thức có dạng vô định hay không trước khi tính giới hạn.
Sử dụng các phương pháp phù hợp để giải quyết từng loại bài tập giới hạn.
Nắm vững các công thức giới hạn đặc biệt để áp dụng khi cần thiết.
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác, như:
Tính đạo hàm và tích phân.
Nghiên cứu sự hội tụ của dãy số và chuỗi số.
Giải quyết các bài toán về vật lý, kinh tế, và các lĩnh vực khác.
Hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ nắm vững kiến thức và tự tin giải bài tập 1.18 trang 15 Sách bài tập Toán 12 - Kết nối tri thức. Chúc các em học tập tốt!