Bài 2.47 trang 57 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.47 trang 57 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
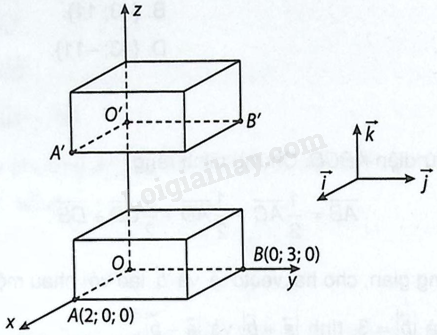
Trên phần mềm GeoGebra 3D với các trục tọa độ được dựng sẵn, bạn Minh vẽ hai hình hộp chữ nhật với một số cạnh đặt dọc theo các trục tọa độ. Ba đỉnh thuộc mặt dưới của hình hộp thứ nhất lần lượt là (Oleft( {0;0;0} right)), (Aleft( {2;0;0} right)), (Bleft( {0;3;0} right)). Biết hình hộp thứ hai ở vị trí cao hơn hình hộp thứ nhất là 5 đơn vị, xác định tọa độ của các đỉnh (O',A',B') thuộc mặt dưới của hình hộp thứ hai.
Đề bài
Trên phần mềm GeoGebra 3D với các trục tọa độ được dựng sẵn, bạn Minh vẽ hai hình hộp chữ nhật với một số cạnh đặt dọc theo các trục tọa độ. Ba đỉnh thuộc mặt dưới của hình hộp thứ nhất lần lượt là \(O\left( {0;0;0} \right)\), \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\). Biết hình hộp thứ hai ở vị trí cao hơn hình hộp thứ nhất là 5 đơn vị, xác định tọa độ của các đỉnh \(O',A',B'\) thuộc mặt dưới của hình hộp thứ hai.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình hộp chữ nhật trong đề để tìm ra các vectơ bằng nhau phù hợp,
sau đó tính toán để tìm tọa độ các điểm.
Lời giải chi tiết
Vì hình hộp thứ hai nằm ngay phía trên hình hộp thứ nhất và cách hình hộp thứ nhất 5 đơn vị nên \(\overrightarrow {OO'} ,\overrightarrow {AA'} ,\overrightarrow {BB'} \) cùng hướng với \(\overrightarrow k \) và có độ dài là 5.
Suy ra \(\overrightarrow {OO'} = \overrightarrow {AA'} = \overrightarrow {BB'} = \left( {0;0;5} \right)\) do đó \(O'\left( {0;0;5} \right)\), \(A'\left( {2;0;5} \right)\) và \(B'\left( {0;3;5} \right)\).
Bài 2.47 trang 57 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập:
Bài 2.47 yêu cầu học sinh tìm đạo hàm của hàm số cho trước và sử dụng đạo hàm để giải quyết một bài toán liên quan đến tốc độ thay đổi của một đại lượng nào đó.
Lời giải chi tiết:
Để giải bài 2.47, ta thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cho trước là f(x) = x2 + 2x + 1. Ta cần tìm đạo hàm của hàm số này.
Áp dụng quy tắc đạo hàm của hàm đa thức, ta có:
f'(x) = 2x + 2
Vậy, đạo hàm của hàm số f(x) = x2 + 2x + 1 là f'(x) = 2x + 2.
Lưu ý:
Mở rộng:
Ngoài bài 2.47, Sách bài tập Toán 12 - Kết nối tri thức còn rất nhiều bài tập khác về đạo hàm. Các em học sinh nên làm đầy đủ các bài tập để nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 2.47 trang 57 Sách bài tập Toán 12 - Kết nối tri thức này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!
Các bài tập tương tự:
Tóm tắt kiến thức:
| Khái niệm | Công thức |
|---|---|
| Đạo hàm | f'(x) = limh→0 (f(x+h) - f(x)) / h |
| Đạo hàm của hàm số f(x) = xn | f'(x) = nxn-1 |
| Đạo hàm của hàm số f(x) = sin(x) | f'(x) = cos(x) |