Bài 5.27 trang 35 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.27 trang 35 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một quả bóng hình cầu có bán kính 2 m được treo lơ lửng trên một mặt đất phẳng. Tâm quả bóng cách mặt đất 10 m. Chọn hệ trục tọa độ Oxyz có gốc tọa độ O là hình chiếu vuông góc của tâm quả cầu trên mặt đất, tia Oz chứa tâm của quả cầu, các trục Ox, Oy thuộc mặt đất như hình vẽ.
Đề bài
Một quả bóng hình cầu có bán kính 2 m được treo lơ lửng trên một mặt đất phẳng. Tâm quả bóng cách mặt đất 10 m. Chọn hệ trục tọa độ Oxyz có gốc tọa độ O là hình chiếu vuông góc của tâm quả cầu trên mặt đất, tia Oz chứa tâm của quả cầu, các trục Ox, Oy thuộc mặt đất như hình vẽ.
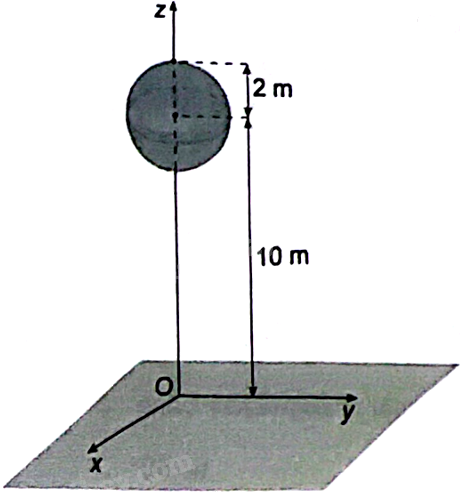
Phương pháp giải - Xem chi tiết
Xác định tâm mặt cầu dựa trên giả thiết tâm thuộc trục Oz và cách mặt đất 10 m.
Lời giải chi tiết
Do tâm quả bóng thuộc tia Oz và cách mặt đất 10 m nên quả cầu có tâm \(I\left( {0;0;10} \right)\).
Bán kính quả bóng bằng 2, do đó ta có phương trình của mặt cầu bề mặt quả bóng là
\({x^2} + {y^2} + {\left( {z - 10} \right)^2} = 4\).
Bài 5.27 trang 35 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Dưới đây là đề bài và lời giải chi tiết bài 5.27 trang 35 Sách bài tập Toán 12 - Kết nối tri thức:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
f'(x) = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | NB | ĐC | NT |
(NB: Nghịch biến, ĐC: Đồng biến, NT: Ngược biến)
Hàm số f(x) đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số f(x) đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Giải thích chi tiết:
Để tìm các điểm cực trị của hàm số, ta thực hiện các bước sau:
Trong bài toán này, ta thấy rằng f'(x) đổi dấu từ dương sang âm tại x = 0, do đó hàm số đạt cực đại tại x = 0.
f'(x) đổi dấu từ âm sang dương tại x = 2, do đó hàm số đạt cực tiểu tại x = 2.
Lưu ý:
Để kiểm tra kết quả, bạn có thể vẽ đồ thị của hàm số f(x) và quan sát các điểm cực trị trên đồ thị.
Ngoài ra, bạn có thể sử dụng các công cụ tính đạo hàm trực tuyến để kiểm tra lại kết quả của mình.
Để luyện tập thêm, bạn có thể giải các bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức, ví dụ như:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về cách giải bài 5.27 trang 35 Sách bài tập Toán 12 - Kết nối tri thức. Chúc bạn học tập tốt!