Bài 1.68 trang 37 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
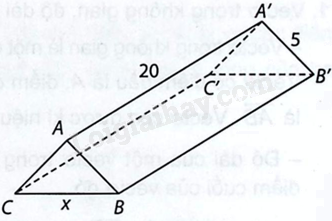
Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng (xem hình bên). Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC. a) Tính thể tích V của hình lăng trụ theo x. b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.
Đề bài
Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng (xem hình bên). Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC.
a) Tính thể tích V của hình lăng trụ theo x.
b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.
Phương pháp giải - Xem chi tiết
Ý a: Sử dụng một số kiến thức về hình học phẳng và hình lăng trụ để tìm được diện tích đáy và chiều cao, từ đó tính được thể tích V.
Ý b: Xét hàm số V theo x trên \(\left( {0;10} \right)\)sau đó lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Lời giải chi tiết
a) Ta thấy do ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật có kích thước giống nhau nên \(AC = AB\) (đều là chiều rộng của mặt hình chữ nhật) do đó đáy \(ABC\)là tam giác cân tại
\(A\). Gọi \(H\) là trung điểm cạnh \(AB\) suy ra \(AH\) là đường cao của tam giác (tính chất tam giác cân). Ta có \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {25 - {{\left( {\frac{x}{2}} \right)}^2}} = \frac{1}{2}\sqrt {100 - {x^2}} \).
Diện tích tam giác ABC là \(S = \frac{1}{2}BC \cdot AH = \frac{1}{2}x \cdot \frac{1}{2}\sqrt {100 - {x^2}} = \frac{1}{4}x\sqrt {100 - {x^2}} \).
Thể tích khối lăng trụ là \(V = S \cdot AA' = 5x\sqrt {100 - {x^2}} \) (m3) với \(0 < x < 10\).
b) Xét hàm số \(V = 5x\sqrt {100 - {x^2}} \) trên \(\left( {0;10} \right)\).
Ta có \(V' = 5x\sqrt {100 - {x^2}} + 5x\frac{{ - 2x}}{{2\sqrt {100 - {x^2}} }} = \frac{{500 - 10{x^2}}}{{\sqrt {100 - {x^2}} }};\)
Suy ra \(V' = 0 \Leftrightarrow 500 - 10{x^2} = 0 \Leftrightarrow x = 5\sqrt 2 \) do \(x > 0\).
Lập bảng biến thiên:
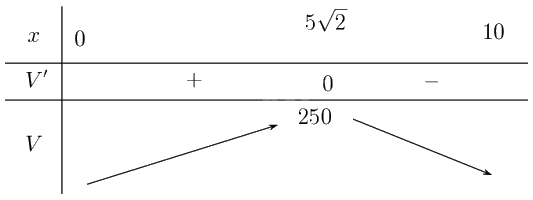
Vậy hình lăng trụ có thể tích lớn nhất khi \(x = 5\sqrt 2 \) (m). \(\mathop {\max }\limits_{\left( {0;10} \right)} V = V\left( {5\sqrt 2 } \right) = 250\) (m3).
Bài 1.68 trang 37 sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 1.68 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Thông thường, hàm số sẽ có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm đã học.
Lời giải chi tiết:
Để giải bài 1.68, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là: f(x) = (x2 + 1) * sin(x)
Áp dụng quy tắc tích, ta có:
f'(x) = (x2 + 1)' * sin(x) + (x2 + 1) * sin'(x)
f'(x) = 2x * sin(x) + (x2 + 1) * cos(x)
Vậy, đạo hàm của hàm số f(x) là: f'(x) = 2x * sin(x) + (x2 + 1) * cos(x)
Lưu ý khi giải bài tập:
Mở rộng kiến thức:
Ngoài bài 1.68, các em học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức để rèn luyện kỹ năng giải bài tập về đạo hàm. Bên cạnh đó, các em cũng có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như việc tìm cực trị của hàm số, vẽ đồ thị hàm số, và giải các bài toán tối ưu hóa.
Tầm quan trọng của việc nắm vững kiến thức về đạo hàm:
Kiến thức về đạo hàm là nền tảng quan trọng cho việc học tập các môn học khác, đặc biệt là Vật lý và Kinh tế. Đạo hàm được sử dụng rộng rãi trong các lĩnh vực khoa học kỹ thuật để mô tả sự thay đổi của các đại lượng và giải quyết các bài toán thực tế. Do đó, việc nắm vững kiến thức về đạo hàm là rất cần thiết cho sự phát triển của học sinh trong tương lai.
Tổng kết:
Bài 1.68 trang 37 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng linh hoạt các quy tắc tính đạo hàm, các em học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự. Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ học tập tốt hơn môn Toán.