Bài 1.36 trang 26 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.36 trang 26 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích (300) cm2, lề trái và lề phải là (2) cm, lề trên và lề dưới là (3) cm. Gọi (x) (cm) là chiều rộng của tờ giấy. a) Tính diện tích của tờ giấy theo (x). b) Kí hiệu diện tích tờ giấy là (Sleft( x right)). Khảo sát sự biến thiên của hàm số (y = Sleft( x right)). c) Tìm kích thước của tờ giấy sao cho nguyên liệu giấy được sử dụng là ít nhất.
Đề bài
Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích \(300\) cm2, lề trái và lề phải là \(2\) cm, lề trên và lề dưới là \(3\) cm. Gọi \(x\) (cm) là chiều rộng của tờ giấy.
a) Tính diện tích của tờ giấy theo \(x\).
b) Kí hiệu diện tích tờ giấy là \(S\left( x \right)\). Khảo sát sự biến thiên của hàm số \(y = S\left( x \right)\).
c) Tìm kích thước của tờ giấy sao cho nguyên liệu giấy được sử dụng là ít nhất.
Phương pháp giải - Xem chi tiết
Ý a:
+ Gọi y là chiều dài, từ diện tích vùng in, biểu diễn \(y\) theo \(x\)
+ Tiếp theo tính diện tích mẫu giấy \(S\left( x \right) = xy\).
Ý b:
+ Khảo sát hàm số \(S\left( x \right)\) trên \(\left( {4; + \infty } \right)\).
Ý c: Tìm giá trị nhỏ nhất của \(S\left( x \right)\) dựa trên bảng biến thiên đã lập ở ý b, tìm giá trị \(x,{\rm{ y}}\)để hàm đạt giá trị nhỏ nhất đó.
Lời giải chi tiết
Gọi \(y\) (cm) là chiều dài của tờ giấy.
Khi đó diện tích vùng in của tờ giấy là \(\left( {x - 4} \right)\left( {y - 6} \right) = 300\) (cm2)
Suy ra \(y = 6 + \frac{{300}}{{x - 4}}\).
a) Diện tích của tờ giấy là \(S\left( x \right) = xy = x\left( {6 + \frac{{300}}{{x - 4}}} \right) = \frac{{x\left( {6x + 276} \right)}}{{x - 4}}\)
b) Tập xác định \(\left( {4; + \infty } \right)\).
Sự biến thiên: \(S\left( x \right) = 6x + 300 + \frac{{1200}}{{x - 4}}\) khi đó \(S'\left( x \right) = \frac{{6{{\left( {x - 4} \right)}^2} - 1200}}{{{{\left( {x - 4} \right)}^2}}}\)
+ Ta có \(S'\left( x \right) = 0 \Leftrightarrow \frac{{6{{\left( {x - 4} \right)}^2} - 1200}}{{{{\left( {x - 4} \right)}^2}}} = 0 \Leftrightarrow 6{\left( {x - 4} \right)^2} - 1200 = 0 \Leftrightarrow x = 4 + 10\sqrt 2 \).
+ Hàm số đồng biến trên khoảng \(\left( {4 + 10\sqrt 2 ; + \infty } \right)\), nghịch biến trên khoảng \(\left( {4;4 + 10\sqrt 2 } \right)\).
+ Hàm số đạt cực tiểu tại \(x = 4 + 10\sqrt 2 \).
+ Bảng biến thiên:
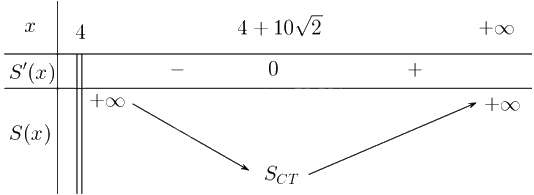
c) Để sử dụng ít nguyên liệu nhất thì tờ giấy có diện tích bé nhất hay \(S\left( x \right)\) nhỏ nhất.
Từ bảng biến thiên ta suy ra \(S\left( x \right)\) nhỏ nhất tại \(x = 4 + 10\sqrt 2 \) suy ra \(y = 6 + \frac{{300}}{{x - 4}} = 6 + \frac{{30}}{{\sqrt 2 }}\). Vậy chiều rộng bằng \(4 + 10\sqrt 2 \), chiều dài bằng \(6 + \frac{{30}}{{\sqrt 2 }}\) thì nguyên liệu giấy được sử dụng ít nhất.
Bài 1.36 trang 26 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 1.36 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Hàm số có thể là một hàm số đơn giản hoặc một hàm số phức tạp được xây dựng từ các hàm số cơ bản bằng các phép toán cộng, trừ, nhân, chia, hợp thành.
Phương pháp giải:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là f(x) = x2 + 2x + 1. Ta có thể tính đạo hàm của hàm số này như sau:
f'(x) = (x2)' + (2x)' + (1)' = 2x + 2 + 0 = 2x + 2
Các dạng bài tập thường gặp:
Lưu ý khi giải bài tập:
Bài giải chi tiết bài 1.36 trang 26 Sách bài tập Toán 12 - Kết nối tri thức:
(Nội dung giải bài tập cụ thể sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng. Bài giải sẽ được trình bày rõ ràng, dễ hiểu để học sinh có thể tự học và nắm vững kiến thức.)
Mở rộng kiến thức:
Ngoài việc giải bài tập, học sinh cũng nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như:
Việc nắm vững kiến thức về đạo hàm sẽ giúp học sinh giải quyết các bài toán Toán 12 một cách hiệu quả và tự tin hơn. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ học tốt môn Toán 12 và đạt kết quả cao trong các kỳ thi.
Tổng kết:
Bài 1.36 trang 26 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Việc nắm vững các quy tắc tính đạo hàm và phương pháp giải bài tập sẽ giúp học sinh tự tin giải quyết các bài toán tương tự trong tương lai.