Bài 3.18 trang 67 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.18 trang 67 SBT Toán 12 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Biểu đồ tần số tương đối ghép nhóm sau cho biết phân bố về khối lượng của 200 bao xi măng trước khi xuất xưởng: a) Lập bảng tần số ghép nhóm cho dữ liệu về khối lượng của 200 bao xi măng trên. b) Tính khoảng tứ phân vị cho mẫu số liệu ghép nhóm thu được ở câu a.
Đề bài
Biểu đồ tần số tương đối ghép nhóm sau cho biết phân bố về khối lượng của 200 bao xi măng trước khi xuất xưởng:
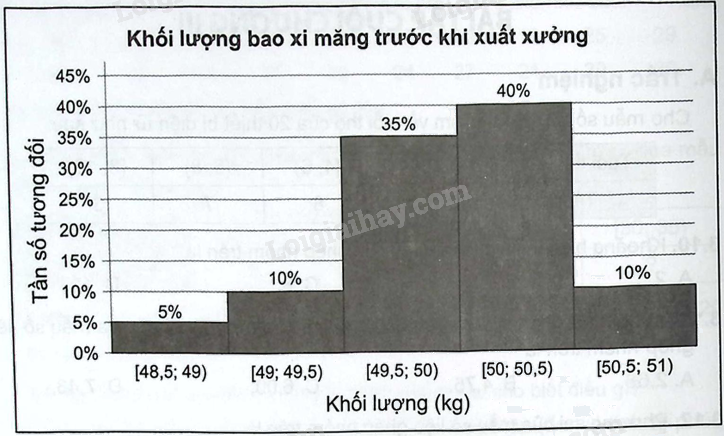
a) Lập bảng tần số ghép nhóm cho dữ liệu về khối lượng của 200 bao xi măng trên.
b) Tính khoảng tứ phân vị cho mẫu số liệu ghép nhóm thu được ở câu a.
Phương pháp giải - Xem chi tiết
Ý a: Lập bảng có 2 hàng, hàng thứ nhất là khối lượng, hàng thứ hai là số bao xi măng. Dữ liệu có trong mỗi ô được xác định từ biểu đồ trong đề bài.
Ý b: Thực hiện từng bước, tìm vị trí, tính \({Q_1}\), \({Q_3}\) sau đó tính khoảng tứ phân vị bằng công thức đã học.
Lời giải chi tiết
a) Từ biểu đồ, ta lập bảng tần số ghép nhóm cho dữ liệu về khối lượng của 200 bao xi măng như sau ( với tần số-số bao xi măng được bằng tổng số bao xi măng là 200 nhân với tỉ lệ phần trăm tương ứng của từng cột trên biểu đồ):
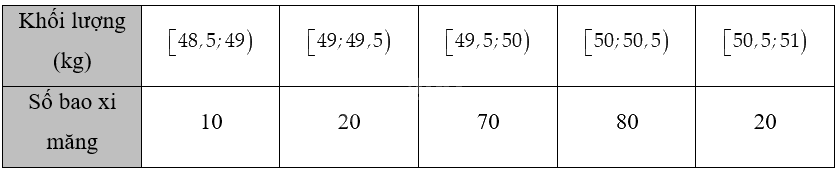
b) Cỡ mẫu là \(n = 200\).
Vị trí của \({Q_1}\) là \(\frac{n}{4} = 50\) suy ra nhóm chứa tứ phân vị thứ nhất là \(\left[ {49,5;50} \right)\).
Ta có \({Q_1} = 49,5 + \frac{{\frac{{1 \cdot 200}}{4} - 30}}{{70}} \cdot 0,5 = \frac{{695}}{{14}}\).
Tương tự có vị trí của \({Q_3}\) là \(\frac{{3n}}{4} = 150\) suy ra nhóm chứa tứ phân vị thứ ba là \(\left[ {50;50,5} \right)\). Do đó \({Q_3} = 50 + \frac{{\frac{{3 \cdot 200}}{4} - 100}}{{80}} \cdot 0,5 = 50,3125\).
Suy ra khoảng tứ phân vị là \({\Delta _Q} = {Q_3} - {Q_1} = 50,3125 - \frac{{695}}{{14}} \approx 0,6696\).
Bài 3.18 trang 67 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 3.18 yêu cầu học sinh tìm đạo hàm của các hàm số được cho. Các hàm số này thường có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm.
Lời giải chi tiết:
Để giải bài 3.18 trang 67 SBT Toán 12 Kết nối tri thức, chúng ta sẽ tiến hành từng bước như sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là: f(x) = x2 + 2x + 1
Áp dụng quy tắc đạo hàm của hàm số đa thức, ta có:
f'(x) = 2x + 2
Lưu ý:
Mở rộng kiến thức:
Ngoài việc giải bài tập, học sinh nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, chẳng hạn như:
Bài tập tương tự:
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Kết luận:
Bài 3.18 trang 67 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng linh hoạt các quy tắc tính đạo hàm, học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập và đạt kết quả tốt trong môn Toán 12.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = x2 | f'(x) = 2x |
| g(x) = sin(x) | g'(x) = cos(x) |