Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài 1.65 trang 36 một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Cho hàm số (y = frac{{left( {m + 1} right)x - 2m + 1}}{{x - 1}}). a) Tìm (m) để tiệm cận ngang của đồ thị đi qua (left( {1;2} right)). b) Khảo sát và vẽ đồ thị (left( H right)) của hàm số (y = fleft( x right)) với (m) tìm được ở câu a. c) Từ đồ thị (left( H right)) của hàm số (y = fleft( x right)) ở câu b, vẽ đồ thị (y = left| {fleft( x right)} right|).
Đề bài
Cho hàm số \(y = \frac{{\left( {m + 1} \right)x - 2m + 1}}{{x - 1}}\).
a) Tìm \(m\) để tiệm cận ngang của đồ thị đi qua \(\left( {1;2} \right)\).
b) Khảo sát và vẽ đồ thị \(\left( H \right)\) của hàm số \(y = f\left( x \right)\) với \(m\) tìm được ở câu a.
c) Từ đồ thị \(\left( H \right)\) của hàm số \(y = f\left( x \right)\) ở câu b, vẽ đồ thị \(y = \left| {f\left( x \right)} \right|\).
Phương pháp giải - Xem chi tiết
Ý a: Tìm tiệm cận ngang sau đó thay giá trị điểm \(\left( {1;2} \right)\) vào phương trình đường thẳng.
Ý b: Khảo sát và vẽ đồ thị hàm số \(\left( H \right)\).
Ý c: Sử dụng công thức hàm giá trị tuyệt đối để rút ra cách vẽ:
\(y = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}f\left( x \right){\rm{ khi f}}\left( x \right) \ge 0\\ - f\left( x \right){\rm{ khi f}}\left( x \right) < 0\end{array} \right.\)
Lời giải chi tiết
a) Tiệm cận ngang của đồ thị hàm số là đường thẳng \(y = m + 1\). Để đường thẳng này đi qua \(\left( {1;2} \right)\) thì \(2 = m + 1 \Leftrightarrow m = 1\).
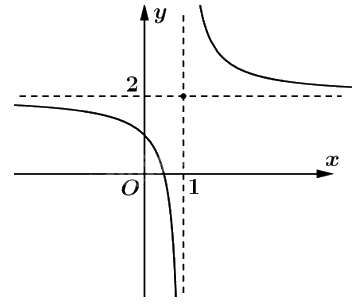
b) Xét đồ thị hàm số \(\left( H \right):{\rm{ }}y = \frac{{2x - 1}}{{x - 1}}\).
Tập xác định: \(\mathbb{R}\backslash \left\{ 1 \right\}\).
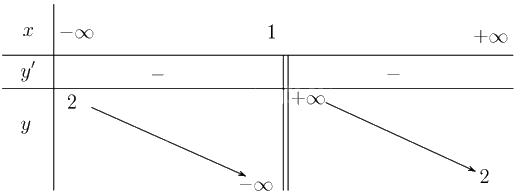
Ta có \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\forall x \ne 1\). Suy ra hàm số nghịch biến trên từng khoảng của tập xác định.
Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{2x - 1}}{{x - 1}} = 2\) suy ra \(y = 2\) là tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 1}}{{x - 1}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x - 1}}{{x - 1}} = - \infty \) suy ra \(x = 1\) là tiệm cận đứng.
Ta lập bảng biến thiên
Đồ thị:
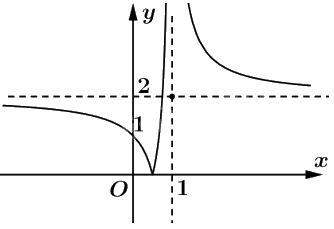
c) Ta có
\(y = \left| {f\left( x \right)} \right| = \left\{ \begin{array}{l}f\left( x \right){\rm{ khi f}}\left( x \right) \ge 0\\ - f\left( x \right){\rm{ khi f}}\left( x \right) < 0\end{array} \right.\)
Để vẽ đồ thị hàm giá trị tuyệt đối ta làm như sau: Giữ nguyên phần đồ thị phía trên trục hoành, lấy đối xứng phần đồ thị nằm dưới trục hoành qua trục hoành.
Bài 1.65 trang 36 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài toán này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài 1.65:
Trước khi bắt đầu giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Đề bài thường cung cấp một hàm số và yêu cầu tính đạo hàm của hàm số đó tại một điểm cụ thể hoặc tìm các điểm cực trị của hàm số.
Để giải bài 1.65, bạn cần nắm vững các công thức và kiến thức sau:
(Giả sử đề bài cụ thể của bài 1.65 là: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
f'(x) = 3x2 - 6x
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
f''(x) = 6x - 6
Tại x = 0: f''(0) = -6 ≠ 0. Vậy hàm số đạt cực đại tại x = 0.
Tại x = 2: f''(2) = 6 ≠ 0. Vậy hàm số đạt cực tiểu tại x = 2.
f(0) = 2 (Giá trị cực đại)
f(2) = -2 (Giá trị cực tiểu)
Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Đạo hàm có rất nhiều ứng dụng trong thực tế, như:
Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ cách giải bài 1.65 trang 36 sách bài tập Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!