Bài 3.19 trang 68 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.19 trang 68 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Bảng thống kê sau cho biết dân số thế giới theo độ tuổi (đơn vị tính là triệu người) trong hai năm 2000 và 2020: a) Chọn 75 là đại diện cho nhóm 65 tuổi trở lên. Hãy ước lượng tuổi trung bình của dân số thế giới trong hai năm 2000 và 2020. b) Tìm khoảng tứ phân vị cho tuổi của dân số thế giới trong hai năm 2000 và 2020. Nêu nhận xét về sự thay đổi cấu trúc dân số theo độ tuổi.
Đề bài
Bảng thống kê sau cho biết dân số thế giới theo độ tuổi (đơn vị tính là triệu người) trong hai năm 2000 và 2020:
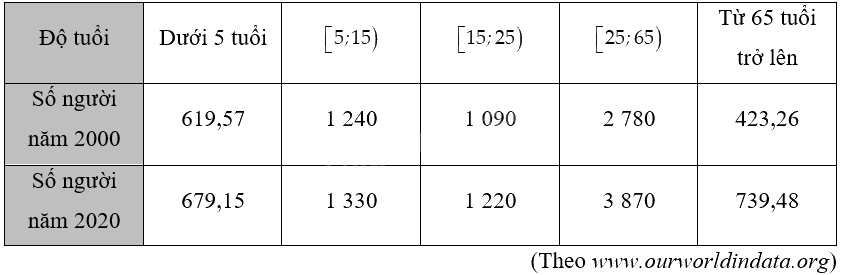
a) Chọn 75 là đại diện cho nhóm 65 tuổi trở lên. Hãy ước lượng tuổi trung bình của dân số thế giới trong hai năm 2000 và 2020.
b) Tìm khoảng tứ phân vị cho tuổi của dân số thế giới trong hai năm 2000 và 2020. Nêu nhận xét về sự thay đổi cấu trúc dân số theo độ tuổi.
Phương pháp giải - Xem chi tiết
Ý a: Chọn giá trị đại diện cho các nhóm số liệu, xét từng mẫu số liệu, tính cỡ mẫu, giá trị trung bình.
Ý b: Thực hiện từng bước, tìm vị trí, tính \({Q_1}\), \({Q_3}\) sau đó tính khoảng tứ phân vị bằng công thức đã học của từng mẫu dữ liệu. Từ sự thay đổi của giá trị trung bình và khoảng tứ phân vị đưa ra nhận xét về sự thay đổi cấu trúc dân số theo độ tuổi qua các năm.
Lời giải chi tiết
a) Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
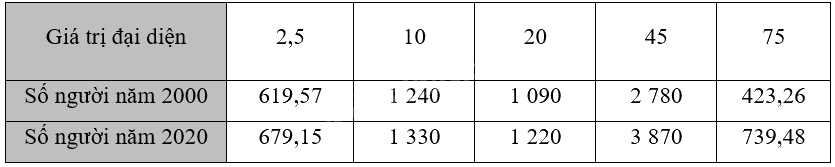
+ Xét mẫu số liệu dân số thế giới theo độ tuổi trong năm 2000:
Cỡ mẫu là \(n = 619,57 + 1240 + 1090 + 2780 + 423,26 = 6152,83\).
Tuổi trung bình của dân số thế giới trong năm 2000 là
\(\begin{array}{l}\overline {{x_{2000}}} = \frac{1}{n}\left( {2,5 \cdot 619,57 + 10 \cdot 1240 + 20 \cdot 1090 + 45 \cdot 2780 + 423,26 \cdot 75} \right)\\ = \frac{1}{n}\left( {1548,925 + 12400 + 21800 + 125100 + 31744,5} \right) = \frac{{192593,425}}{{6152,83}} \approx 31,3016.\end{array}\)
+ Xét mẫu số liệu dân số thế giới theo độ tuổi trong năm 2020:
Cỡ mẫu là \(n = 679,15 + 1330 + 1220 + 3870 + 739,48 = 7838,63\).
Tuổi trung bình của dân số thế giới trong năm 2020 là
\(\begin{array}{l}\overline {{x_{2020}}} = \frac{1}{n}\left( {2,5 \cdot 679,15 + 10 \cdot 1330 + 20 \cdot 1220 + 45 \cdot 3870 + 739,48 \cdot 75} \right)\\ = \frac{1}{n}\left( {1697,875 + 13300 + 24400 + 174150 + 55461} \right) = \frac{{269008,875}}{{7838,63}} \approx 34,3184.\end{array}\)
b) + Xét mẫu số liệu dân số thế giới theo độ tuổi trong năm 2000:
Cỡ mẫu là \(n = 6152,83\).
Vị trí của \({Q_1}\) là \(\frac{n}{4} = 1538,2075\) suy ra nhóm chứa tứ phân vị thứ nhất là \(\left[ {5;15} \right)\).
Ta có \({Q_1} = 5 + \frac{{1538,2075 - 619,57}}{{1240}} \cdot 10 \approx 12,4084\).
Tương tự có vị trí của \({Q_3}\) là \(\frac{{3n}}{4} = 4614,6225\) suy ra nhóm chứa tứ phân vị thứ ba là \(\left[ {25;65} \right)\)Do đó \({Q_3} = 25 + \frac{{4614,6225 - \left( {619,57 + 1240 + 1090} \right)}}{{2780}} \cdot 40 = 48,9576\).
Suy ra khoảng tứ phân vị là \({\Delta _Q} = {Q_3} - {Q_1} \approx 48,9576 - 12,4084 = 36,5492\).
+ Xét mẫu số liệu dân số thế giới theo độ tuổi trong năm 2020:
Cỡ mẫu là \(n = 7838,63\).
Vị trí của \({Q_1}\) là \(\frac{n}{4} = 1959,6575\) suy ra nhóm chứa tứ phân vị thứ nhất là \(\left[ {5;15} \right)\).
Ta có \({Q_1} = 5 + \frac{{1959,6575 - 679,15}}{{1330}} \cdot 10 \approx 14,6279\).
Tương tự có vị trí của \({Q_3}\) là \(\frac{{3n}}{4} = 5878,9725\) suy ra nhóm chứa tứ phân vị thứ ba là \(\left[ {25;65} \right)\)Do đó \({Q_3} = 25 + \frac{{5878,9725 - \left( {679,15 + 1330 + 1220} \right)}}{{3870}} \cdot 40 = 52,3883\).
Suy ra khoảng tứ phân vị là \({\Delta _Q} = {Q_3} - {Q_1} \approx 52,3883 - 14,6279 = 37,7604\).
Ta thấy, từ năm 2000 đến năm 2020 tuổi trung bình của dân số thế giới đã tăng từ \(31,3016\) đến \(34,3184\), điều này phản ánh sự già hóa của dân số, dân số thế giới năm 2020 già hơn. Ngoài ra, dân số thế giới năm 2020 có độ tuổi phân tán hơn so với dân số thế giới năm 2000.
Bài 3.19 trang 68 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập:
Bài 3.19 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Thông thường, hàm số sẽ có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm đã học.
Lời giải chi tiết:
Để giải bài 3.19, ta thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là: y = sin(x2 + 1)
Ta thực hiện như sau:
Đạo hàm của hàm số bên ngoài: (sin(u))' = cos(u)
Đạo hàm của hàm số bên trong: (x2 + 1)' = 2x
Áp dụng quy tắc đạo hàm hợp: y' = cos(x2 + 1) * 2x = 2x * cos(x2 + 1)
Lưu ý:
Khi giải bài tập về đạo hàm, cần chú ý đến các quy tắc đạo hàm và áp dụng chúng một cách chính xác. Ngoài ra, cần rèn luyện kỹ năng rút gọn biểu thức để có được kết quả cuối cùng đơn giản nhất.
Các bài tập tương tự:
Để củng cố kiến thức về đạo hàm, học sinh có thể làm thêm các bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức. Các bài tập này sẽ giúp học sinh hiểu sâu hơn về các quy tắc đạo hàm và rèn luyện kỹ năng giải bài tập.
Tài liệu tham khảo:
Kết luận:
Bài 3.19 trang 68 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng linh hoạt các quy tắc đạo hàm, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh học tập tốt hơn môn Toán 12.
| Hàm số | Đạo hàm |
|---|---|
| y = xn | y' = nxn-1 |
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |