Bài 1.49 trang 32 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình. b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm: (i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa; (ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bì
Đề bài
a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình.
b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm:
(i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa;
(ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bình;
(iii) Chi phí trung bình nhỏ nhất.
Phương pháp giải - Xem chi tiết
Ý a: Tính \(\overline {C'} \left( x \right)\), sử dụng ý nghĩa của cực tiểu để chứng minh.
Ý b: Xác định công thức các hàm \(\overline C \left( x \right)\), \(C'\left( x \right)\).
(i) Thay \(x = 100\) vào các hàm \(C\left( x \right)\), \(\overline C \left( x \right)\), \(C'\left( x \right)\).
(ii) Khảo sát sự biến thiên của hàm \(\overline C \left( x \right)\), xác định khoảng mà hàm nghịch biến từ đó ruy ra mức sản xuất x.
(iii) Tìm giá trị nhỏ nhất của hàm số \(\overline C \left( x \right)\).
Lời giải chi tiết
a) Ta có \(\overline {C'} \left( x \right) = {\left[ {\frac{{C\left( x \right)}}{x}} \right]^\prime } = \frac{{C'\left( x \right) \cdot x - C\left( x \right)}}{{{x^2}}}\).
Chi phí trung bình nhỏ nhất khi \(\overline {C'} \left( x \right) = 0\) hay \(C'\left( x \right) \cdot x - C\left( x \right) = 0 \Leftrightarrow C'\left( x \right) = \frac{{C\left( x \right)}}{x}\).
Nói cách khác chi phí biên bằng chi phí trung bình.
b) Xét hàm số \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\).
Ta có hàm chi phí trung bình là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{16000 + 200x + 4{x^{\frac{3}{2}}}}}{x} = \frac{{16000}}{x} + 200 + 4{x^{\frac{1}{2}}}\).
Hàm chi phí biên là \(C'\left( x \right) = 200 + 6{x^{\frac{1}{2}}}\).
(i) Ta có \(C\left( {100} \right) = 16000 + 200 \cdot 100 + 4 \cdot {100^{\frac{3}{2}}} = 40000\); \(\overline C \left( {100} \right) = \frac{{16000}}{{100}} + 200 + 4 \cdot {100^{\frac{1}{2}}} = 400\);
\(C'\left( {100} \right) = 200 + 6 \cdot {100^{\frac{1}{2}}} = 260\).
Vậy chi phí, chi phí trung bình và chi phí biên ở mức sản xuất 100 đơn vị hàng hóa lần lượt là \(40000\) USD, \(400\) USD và \(260\) USD.
(ii) Ta có \(\overline {C'} \left( x \right) = \frac{{ - 16000}}{{{x^2}}} + 2{x^{ - \frac{1}{2}}}\) khi đó \(\overline {C'} \left( x \right) = 0 \Leftrightarrow \frac{{ - 16000}}{{{x^2}}} + 2{x^{ - \frac{1}{2}}} = 0 \Leftrightarrow x = 400\) do \(x > 0\).
Lập bảng biến thiên
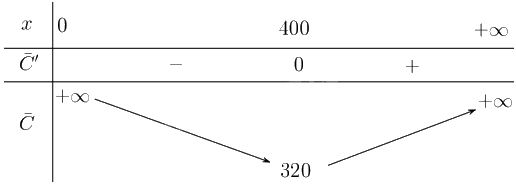
Từ bảng biến thiên suy ra, mức sản xuất là 400 đơn vị hàng hóa thì sẽ giảm thiểu giá trị trung bình.
(iii) Chi phí trung bình nhỏ nhất là 320 USD.
Bài 1.49 trang 32 sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 1.49 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Thông thường, hàm số sẽ có dạng phức tạp, đòi hỏi học sinh phải áp dụng nhiều quy tắc tính đạo hàm khác nhau.
Lời giải chi tiết:
Để giải bài 1.49, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là: f(x) = (x2 + 1) * sin(x)
Áp dụng quy tắc nhân, ta có:
f'(x) = (x2 + 1)' * sin(x) + (x2 + 1) * sin'(x)
f'(x) = 2x * sin(x) + (x2 + 1) * cos(x)
Vậy, đạo hàm của hàm số f(x) là: f'(x) = 2x * sin(x) + (x2 + 1) * cos(x)
Các dạng bài tập tương tự:
Ngoài bài 1.49, còn rất nhiều bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức. Các bài tập này thường yêu cầu học sinh:
Mẹo giải bài tập đạo hàm:
Tầm quan trọng của việc học đạo hàm:
Đạo hàm là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong các lĩnh vực khác nhau, như vật lý, kinh tế, kỹ thuật. Việc nắm vững kiến thức về đạo hàm giúp học sinh:
Kết luận:
Bài 1.49 trang 32 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.