Bài 2.21 trang 49 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.21 trang 49, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp tứ giác đều (S.ABCD) có chiều cao bằng 5 và độ dài cạnh đáy bằng 4. Hãy xác định tọa độ các điểm (S,A,B,C,D) đối với hệ tọa độ (Oxyz) có gốc (O) trùng với tâm của hình vuông (ABCD), tia (Ox) chứa (B), tia (Oy) chứa (C) và tia (Oz) chứa (S).
Đề bài
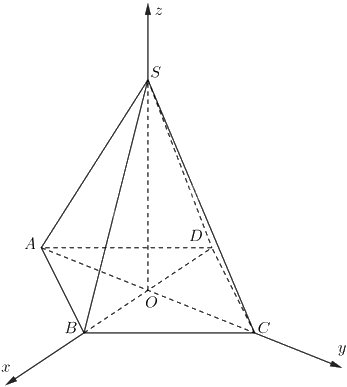
Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao bằng 5 và độ dài cạnh đáy bằng 4. Hãy xác định tọa độ các điểm \(S,A,B,C,D\) đối với hệ tọa độ \(Oxyz\) có gốc \(O\) trùng với tâm của hình vuông \(ABCD\), tia \(Ox\) chứa \(B\), tia \(Oy\) chứa \(C\) và tia \(Oz\) chứa \(S\).
Lập hệ trục tọa độ theo giả thiết và xác định tọa độ từng điểm.
Phương pháp giải - Xem chi tiết
Lời giải chi tiết
Ta có \(S\) thuộc tia \(Oz\) và \(OS = 5\) nên \(S\left( {0;0;5} \right)\).
Do \(ABCD\) là hình vuông cạnh \(4\) nên \(OA = OB = OC = OD = 2\sqrt 2 \).
Ta có \(B\) thuộc tia \(Ox\) và \(OB = 2\sqrt 2 \) suy ra \(B\left( {2\sqrt 2 ;0;0} \right)\); \(D\) thuộc tia đối của tia \(Ox\) và \(OD = 2\sqrt 2 \) suy ra \(D\left( { - 2\sqrt 2 ;0;0} \right)\).
Tương tự có \(C\) thuộc tia \(Oy\) và \(OC = 2\sqrt 2 \) suy ra \(C\left( {0;2\sqrt 2 ;0} \right)\); \(A\) thuộc tia đối của tia \(Oy\) và \(OA = 2\sqrt 2 \) suy ra \(A\left( {0; - 2\sqrt 2 ;0} \right)\).
Vậy \(S\left( {0;0;5} \right)\), \(A\left( {0; - 2\sqrt 2 ;0} \right)\), \(B\left( {2\sqrt 2 ;0;0} \right)\), \(C\left( {0;2\sqrt 2 ;0} \right)\) và \(D\left( { - 2\sqrt 2 ;0;0} \right)\).
Bài 2.21 trang 49 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài toán:
Bài 2.21 yêu cầu học sinh tìm đạo hàm của hàm số và sử dụng đạo hàm để giải quyết các bài toán liên quan đến tính chất của hàm số (tăng, giảm, cực trị).
Để giải bài 2.21 trang 49, chúng ta thực hiện theo các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta sẽ áp dụng các bước trên để giải bài toán:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 2.21 trang 49 sách bài tập Toán 12 Kết nối tri thức và đạt kết quả tốt trong môn học.
Ngoài ra, các em có thể tham khảo thêm các bài giải khác trên Giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải toán.