Bài 1.16 trang 15 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.16 trang 15 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Lợi nhuận thu được (P) của một công ty khi dùng số tiền (s) chi cho quảng cáo được cho bởi công thức (P = Pleft( s right) = - frac{1}{{10}}{s^3} + 6{s^2} + 400,{rm{ s}} ge 0). Ở đây các số tiền được được tính bằng đơn vị nghìn USD. a) Tìm số tiền công ty phải chi cho quảng cáo để mang lại lợi nhuận tối đa. b) Lợi nhuận thu được của công ty thay đổi thế nào khi số tiền chi cho quảng cáo thay đổi?
Đề bài
Lợi nhuận thu được \(P\) của một công ty khi dùng số tiền \(s\) chi cho quảng cáo được cho bởi công thức
\(P = P\left( s \right) = - \frac{1}{{10}}{s^3} + 6{s^2} + 400,{\rm{ s}} \ge 0\).
Ở đây các số tiền được được tính bằng đơn vị nghìn USD.
a) Tìm số tiền công ty phải chi cho quảng cáo để mang lại lợi nhuận tối đa.
b) Lợi nhuận thu được của công ty thay đổi thế nào khi số tiền chi cho quảng cáo thay đổi?
Phương pháp giải - Xem chi tiết
Ý a: Yêu cầu bài toán tương đương với việc tìm \({\rm{s}}\) để hàm \(P\left( s \right) = - \frac{1}{{10}}{s^3} + 6{s^2} + 400,{\rm{ s}} \ge 0\) đạt giá trị lớn nhất. Sử dụng cách lập bảng biến thiên để xác định giá trị lớn nhất \(\mathop {\max }\limits_{\left[ {0; + \infty } \right)} P\left( s \right)\).
Ý b: Từ bảng biến thiên ý a biết được các khoảng đồng biến, nghịch biến của hàm số, từ đó đưa ra các nhận xét về sự thay đổi (tăng/giảm) của số tiền chi cho quảng cáo \(s\) ảnh hưởng như thế nào đến lợi nhuận \(P\left( s \right)\).
Lời giải chi tiết
a) Xét hàm số \(P\left( s \right) = - \frac{1}{{10}}{s^3} + 6{s^2} + 400,{\rm{ s}} \ge 0\), ta cần tìm \(s \ge 0\) để \(P\left( s \right)\) đạt giá trị lớn nhất.
Ta có: \(P'\left( s \right) = - \frac{3}{{10}}{s^2} + 12s\). Khi đó \(P' = 0 \Leftrightarrow - \frac{3}{{10}}{s^2} + 12s = 0 \Leftrightarrow s = 0\) hoặc \(s = 40\).
Lập bảng biến thiên của hàm số:
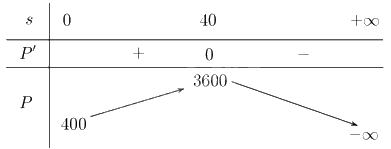
Từ bảng biến thiên ta có \(\mathop {\max }\limits_{\left[ {0; + \infty } \right)} P\left( s \right) = P\left( {40} \right) = 3600\). Vậy để mang lại lợi nhuận tối đa, số tiền công ty phải chi trả cho quảng cáo là \(40\) nghìn USD.
b) Từ bảng biến thiên ta thấy hàm số \(P\left( s \right)\) đồng biến trên khoảng \(\left( {0;40} \right)\), nghịch biến trên \(\left( {40; + \infty } \right)\), do đó:
+ Lợi nhuận công ty tăng dần khi số tiền chi cho quảng cáo tăng từ \(0\) đến \(40\) nghìn USD.
+ Lợi nhuận công ty giảm dần khi số tiền chi cho quảng cáo lớn hơn \(40\) nghìn USD và khi đó càng tăng tiền quảng cáo thì lợi nhuận càng giảm.
Bài 1.16 thuộc chương trình Toán 12, sách Kết nối tri thức, tập trung vào việc rèn luyện kỹ năng tính giới hạn của hàm số. Đây là một phần kiến thức nền tảng, quan trọng để học sinh có thể tiếp cận các khái niệm nâng cao hơn trong chương trình Toán học.
Bài tập 1.16 thường bao gồm các dạng bài sau:
Để giải bài tập 1.16 một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Dưới đây là lời giải chi tiết cho bài 1.16 trang 15 Sách bài tập Toán 12 - Kết nối tri thức:
lim (x→2) (x^2 - 4) / (x - 2)
Giải:
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
lim (x→∞) (2x + 1) / (x - 3)
Giải:
lim (x→∞) (2x + 1) / (x - 3) = lim (x→∞) (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
lim (x→0) sin(x) / x
Giải:
lim (x→0) sin(x) / x = 1 (Đây là giới hạn lượng giác cơ bản)
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác, bao gồm:
Bài 1.16 trang 15 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn của hàm số. Việc nắm vững các phương pháp giải và lưu ý khi giải bài tập sẽ giúp học sinh tự tin làm bài tập và đạt kết quả tốt trong môn Toán.