Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 4.8 trang 8 sách bài tập Toán 12 chương trình Kết nối tri thức. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 4.8 trang 8 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất với vận tốc tại thời điểm t (t=0 là thời điểm viên đạn được bắn lên) cho bởi (vleft( t right) = 150 - 9,8t) (m/s). Tìm độ cao của viên đạn (tính từ mặt đất): a) Sau (t = 3) giây; b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất của mét).
Đề bài
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất với vận tốc tại thời điểm t (t=0 là thời điểm viên đạn được bắn lên) cho bởi \(v\left( t \right) = 150 - 9,8t\) (m/s).
Tìm độ cao của viên đạn (tính từ mặt đất):
a) Sau \(t = 3\) giây;
b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất của mét).
Phương pháp giải - Xem chi tiết
Ý a: Độ cao \(h\left( t \right)\) của viên đạn tại thời điểm \(t\) là một nguyên hàm của hàm vận tốc \(v\left( t \right)\).
Tìm \(h\left( t \right)\) sau đó tính \(h\left( 3 \right)\).
Ý b: Tìm giá trị lớn nhất của \(h\left( t \right)\) với \(t \ge 0\). Lập bảng biến thiên để tìm.
Lời giải chi tiết
a) Độ cao \(h\left( t \right)\) của viên đạn tại thời điểm \(t\) là một nguyên hàm của hàm vận tốc \(v\left( t \right)\).
Ta có \(h\left( t \right) = \int {\left( {150 - 9,8t} \right)} dt = 150t - 4,9{t^2} + C\).
Do \(t = 0\) là thời điểm viên đạn được bắn lên nên \(h\left( 0 \right) = 0\).
Suy ra \(150 \cdot 0 - 4,9 \cdot {0^2} + C = 0 \Leftrightarrow C = 0 \Leftrightarrow \)\(h\left( t \right) = 150t - 4,9{t^2}\).
Độ cao của viên đạn sau 3 giây là \(h\left( 3 \right) = 150 \cdot 3 - 4,9 \cdot {3^2} = 405,9\) (m).
b) Độ cao lớn nhất của viên đạn là giá trị lớn nhất của hàm số \(h\left( t \right) = 150t - 4,9{t^2}\) với \(t \ge 0\).
Ta có \(h'\left( t \right) = 150 - 9,8t\) suy ra \(h'\left( t \right) = 0 \Leftrightarrow 150 - 9,8t = 0 \Leftrightarrow t = \frac{{750}}{{49}}\).
Ta lập bảng biến thiên
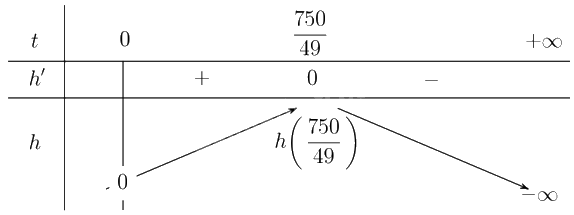
Từ bảng biến thiên suy ra \(\mathop {\max }\limits_{\left[ {0; + \infty } \right)} h\left( t \right) = h\left( {\frac{{750}}{{49}}} \right) = \frac{{56250}}{{49}} \approx 1147,96\).
Vậy viên đạt đạt độ cao lớn nhất khoảng \(1147,96\) m tại thời điểm \(t = \frac{{750}}{{49}}\) giây.
Bài 4.8 trang 8 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Bài tập 4.8 thường bao gồm các dạng bài sau:
Để giải bài 4.8 trang 8 sách bài tập Toán 12 Kết nối tri thức hiệu quả, bạn cần:
Bài toán: Tính đạo hàm của hàm số y = x3 + 2x2 - 5x + 1.
Giải:
Sử dụng quy tắc tính đạo hàm của tổng, hiệu, tích, thương và quy tắc lũy thừa, ta có:
y' = 3x2 + 4x - 5.
Vậy, đạo hàm của hàm số y = x3 + 2x2 - 5x + 1 là y' = 3x2 + 4x - 5.
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 4.8 trang 8 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp bạn rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong các kỳ thi.