Bài 1.38 trang 26 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.38 trang 26 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho điểm (Aleft( {3;2} right)) trên mặt phẳng tọa độ. Một đường thẳng đi qua (A) cắt trục hoành tại (B), cắt trục tung tại (C) tạo thành một tam giác (OBC) nằm trong góc phần tư thứ nhất, với (O) là gốc tọa độ. a) Biết hoành độ điểm (B) là (x = t) với (t > 3). Tính diện tích tam giác (OBC) theo (t). Kí hiệu diện tích này là (Sleft( t right)). b) Khảo sát sự biến thiên của hàm số (Sleft( t right)). c) Tìm vị trí điểm (B) để diện tích tam giác (OBC) nhỏ nhất.
Đề bài
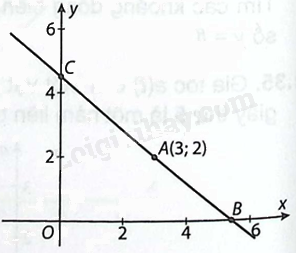
Cho điểm \(A\left( {3;2} \right)\) trên mặt phẳng tọa độ. Một đường thẳng đi qua \(A\) cắt trục hoành tại \(B\), cắt trục tung tại \(C\) tạo thành một tam giác \(OBC\) nằm trong góc phần tư thứ nhất, với \(O\) là gốc tọa độ.
a) Biết hoành độ điểm \(B\) là \(x = t\) với \(t > 3\). Tính diện tích tam giác \(OBC\) theo \(t\). Kí hiệu diện tích này là \(S\left( t \right)\).
b) Khảo sát sự biến thiên của hàm số \(S\left( t \right)\).
c) Tìm vị trí điểm \(B\) để diện tích tam giác \(OBC\) nhỏ nhất.
Phương pháp giải - Xem chi tiết
Ý a:
+ Viết phương trình chính tắc đường thẳng đi qua hai điểm \(A\) và \(B\) với \(A\left( {3;2} \right);B\left( {t;0} \right)\).
+ Biểu diễn \(y\) theo \(x\) và \(t\), từ đó suy ra tung độ của C theo \(t\).
+ Tìm được diện tích \(S\left( t \right) = t \cdot {y_C}\).
Ý b: Khảo sát hàm số \(S\left( t \right)\).
Ý c: Từ bảng biến thiên suy ra giá trị nhỏ nhất của hàm số.
Lời giải chi tiết
a) Đường thẳng đi qua \(A\) và \(B\) có phương trình \(\frac{{y - 2}}{{ - 2}} = \frac{{x - 3}}{{t - 3}}\) hay \(y = 2 - \frac{2}{{t - 3}}\left( {x - 3} \right)\).
Suy ra \(C\) có tung độ là \({y_C} = 2 - \frac{2}{{t - 3}}\left( {0 - 3} \right) = 2 + \frac{6}{{t - 3}}\).
Diện tích tam giác \(OBC\) là \(S\left( t \right) = t \cdot {y_C} = \frac{{2{t^2}}}{{t - 3}}\).
b) Xét hàm số \(S\left( t \right) = \frac{{2{t^2}}}{{t - 3}}\).
Tập xác định: \(\left( {3; + \infty } \right)\).
Sự biến thiên: \(S'\left( t \right) = {\left( {\frac{{2{t^2}}}{{t - 3}}} \right)^\prime } = \frac{{2{t^2} - 12t}}{{{{\left( {t - 3} \right)}^2}}}\).
Khi đó \(S'\left( t \right) = 0 \Leftrightarrow \frac{{2{t^2} - 12t}}{{{{\left( {t - 3} \right)}^2}}} = 0 \Leftrightarrow 2{t^2} - 12t = 0 \Leftrightarrow t = 6\) do \(t > 3\).
+ Hàm số đồng biến trên khoảng \(\left( {6; + \infty } \right)\), nghịch biến trên khoảng \(\left( {3;6} \right)\).
+ Hàm số đạt cực tiểu tại \(t = 6\) với \({S_{CT}} = 24\).
+ Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = + \infty \)
+ Bảng biến thiên:
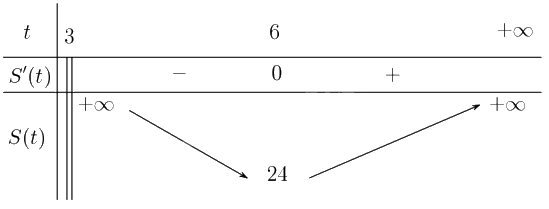
c) Để diện tích tam giác \(OBC\) nhỏ nhất thì \(S\left( t \right)\) đạt giá trị nhỏ nhất.
Từ bảng biến thiên suy ra, giá trị nhỏ nhất của tam giác \(OBC\) là \(24\) khi \(t = 6\) khi đó \(B\left( {0;6} \right)\)
Bài 1.38 trang 26 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 1.38 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Thông thường, hàm số sẽ có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm đã học.
Để giải bài 1.38 trang 26 Sách bài tập Toán 12 - Kết nối tri thức, chúng ta thực hiện theo các bước sau:
Giả sử hàm số cần tìm đạo hàm là: f(x) = 2x3 + sin(x) - ex
Áp dụng các quy tắc tính đạo hàm, ta có:
f'(x) = 6x2 + cos(x) - ex
Ngoài bài 1.38, học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức để nâng cao khả năng giải quyết các bài toán về đạo hàm. Bên cạnh đó, việc tìm hiểu các ứng dụng của đạo hàm trong thực tế (ví dụ: tính vận tốc, gia tốc, tối ưu hóa) sẽ giúp học sinh hiểu sâu hơn về tầm quan trọng của đạo hàm trong Toán học và các lĩnh vực khác.
Để củng cố kiến thức, bạn có thể thử giải các bài tập sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn giải bài 1.38 trang 26 Sách bài tập Toán 12 - Kết nối tri thức, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |