Bài 1.37 trang 26 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.37 trang 26, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Giả sử chi phí để sản xuất (x) sản phẩm của một nhà máy được cho bởi (Cleft( x right) = 0,2{x^2} + 10x + 5) (triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là (fleft( x right) = frac{{Cleft( x right)}}{x}). a) Khảo sát sự biến thiên của hàm số (y = fleft( x right)). b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?
Đề bài
Giả sử chi phí để sản xuất \(x\) sản phẩm của một nhà máy được cho bởi \(C\left( x \right) = 0,2{x^2} + 10x + 5\) (triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\).
a) Khảo sát sự biến thiên của hàm số \(y = f\left( x \right)\).
b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?
Phương pháp giải - Xem chi tiết
Ý a: Khảo sát hàm số \(y = f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{0,2{x^2} + 10x + 5}}{x}\) theo các bước đã học.
Ý b: Từ bảng biến thiên suy ra giá trị nhỏ nhất của hàm số.
Lời giải chi tiết
a) Xét hàm số \(y = f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{0,2{x^2} + 10x + 5}}{x}\) .
Tập xác định \(\left[ {1; + \infty } \right)\).
Sự biến thiên: \(f'\left( x \right) = {\left( {\frac{{0,2{x^2} + 10x + 5}}{x}} \right)^\prime } = \frac{{0,2{x^2} - 5}}{{{x^2}}}\).
Khi đó \(f'\left( x \right) = 0 \Leftrightarrow \frac{{0,2{x^2} - 5}}{{{x^2}}} = 0 \Leftrightarrow x = 5\) do \(x \ge 1\).
+ Ta có \(S'\left( x \right) = 0 \Leftrightarrow \frac{{6{{\left( {x - 4} \right)}^2} - 1200}}{{{{\left( {x - 4} \right)}^2}}} = 0 \Leftrightarrow 6{\left( {x - 4} \right)^2} - 1200 = 0 \Leftrightarrow x = 4 + 10\sqrt 2 \).
+ Hàm số đồng biến trên khoảng \(\left( {5; + \infty } \right)\), nghịch biến trên khoảng \(\left( {1;5} \right)\).
+ Hàm số đạt cực tiểu tại \(x = 5\) với \({f_{CT}} = 12\).
+ Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \)
+ Bảng biến thiên:
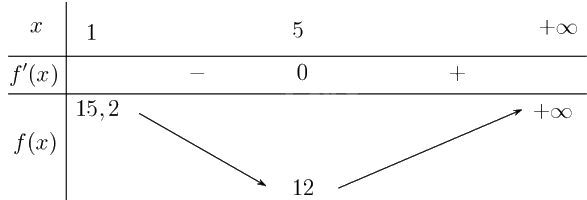
b) Từ bảng biến thiên suy ra số lượng sản phẩm cần sản xuất là \(x = 5\) để chi phí sản xuất trung bình là thấp nhất: \({f_{CT}} = 12\).
Bài 1.37 trang 26 sách bài tập Toán 12 Kết nối tri thức là một bài toán ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Để giải bài toán này, học sinh cần nắm vững các kiến thức về đạo hàm của hàm số, điều kiện cần và đủ để hàm số đạt cực trị, và cách sử dụng đạo hàm để khảo sát hàm số.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một vật thể chuyển động theo quy luật s = t^3 - 3t^2 + 5t + 2, trong đó t là thời gian tính bằng giây và s là quãng đường tính bằng mét. Hãy tìm vận tốc và gia tốc của vật tại thời điểm t = 2.)
Để giải bài toán này, ta thực hiện các bước sau:
Vận tốc của vật là đạo hàm của quãng đường theo thời gian: v(t) = s'(t). Gia tốc của vật là đạo hàm của vận tốc theo thời gian: a(t) = v'(t) = s''(t).
Tính đạo hàm bậc nhất và bậc hai của hàm số quãng đường s(t) = t^3 - 3t^2 + 5t + 2.
s'(t) = 3t^2 - 6t + 5
s''(t) = 6t - 6
Thay t = 2 vào các công thức vận tốc và gia tốc:
v(2) = 3(2)^2 - 6(2) + 5 = 12 - 12 + 5 = 5 (m/s)
a(2) = 6(2) - 6 = 12 - 6 = 6 (m/s^2)
Vậy vận tốc của vật tại thời điểm t = 2 là 5 m/s và gia tốc của vật tại thời điểm t = 2 là 6 m/s^2.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 Kết nối tri thức và các tài liệu luyện thi THPT Quốc gia.
Khi giải bài tập về đạo hàm, các em cần chú ý:
Giaitoan.edu.vn là website học Toán online uy tín, cung cấp đầy đủ các bài giải chi tiết, dễ hiểu, giúp các em học sinh học Toán 12 hiệu quả. Chúng tôi luôn cập nhật các bài giảng mới nhất và đáp ứng mọi nhu cầu học tập của các em.
Hy vọng với lời giải chi tiết bài 1.37 trang 26 sách bài tập Toán 12 Kết nối tri thức này, các em sẽ hiểu rõ hơn về phương pháp giải và tự tin làm bài tập. Chúc các em học tốt!