Bài 4.39 trang 20 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.39 trang 20 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hãy cùng theo dõi lời giải chi tiết dưới đây!
Cho (S) là diện tích phần hình phẳng được tô màu như Hình 4.7. Khi đó diện tích (S) là A. (S = intlimits_a^b {left| {fleft( x right) - gleft( x right)} right|dx} ). B. (S = intlimits_a^m {left| {fleft( x right) - gleft( x right)} right|dx} + intlimits_m^b {left| {gleft( x right) - fleft( x right)} right|dx} ). C. (S = intlimits_a^m {left| {fleft( x right)} right|dx} + intlimits_m^b {left| {gleft( x right)} right|dx} ). D. (S = i
Đề bài
Cho \(S\) là diện tích phần hình phẳng được tô màu như Hình 4.7.
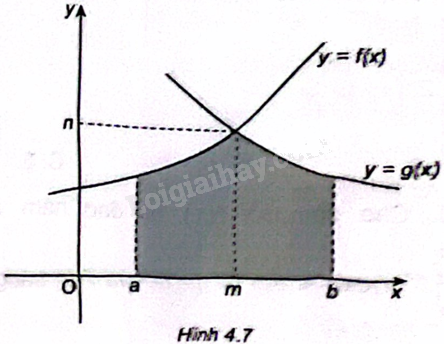
Khi đó diện tích \(S\) là
A. \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
B. \(S = \int\limits_a^m {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + \int\limits_m^b {\left| {g\left( x \right) - f\left( x \right)} \right|dx} \).
C. \(S = \int\limits_a^m {\left| {f\left( x \right)} \right|dx} + \int\limits_m^b {\left| {g\left( x \right)} \right|dx} \).
D. \(S = \int\limits_a^m {\left| {g\left( x \right)} \right|dx} + \int\limits_m^b {\left| {f\left( x \right)} \right|dx} \).
Phương pháp giải - Xem chi tiết
Xét hình phẳng đang cần tìm diện tích, ta chia hình thành hai hình nhỏ và tính diện tích từng hình. \({S_1}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = f\left( x \right)\), trục \(Ox\), đường thẳng \(x = a,x = m\) và \({S_2}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = g\left( x \right)\), trục \(Ox\), đường thẳng \(x = m,x = b\). Áp dụng công thức tính diện tích ứng dụng tích phân đã học.
Lời giải chi tiết
Từ hình vẽ ta thấy \(S = {S_1} + {S_2}\), trong đó \({S_1}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = f\left( x \right)\), trục \(Ox\), đường thẳng \(x = a,x = m\) và \({S_2}\) là diện tích hình phẳng được giới hạn bởi đồ thị \(y = g\left( x \right)\), trục \(Ox\), đường thẳng \(x = m,x = b\).
Ta có \({S_1} = \int\limits_a^m {\left| {f\left( x \right)} \right|dx} \) và \({S_2} = \int\limits_m^b {\left| {g\left( x \right)} \right|dx} \) suy ra \(S = \int\limits_a^m {\left| {f\left( x \right)} \right|dx} + \int\limits_m^b {\left| {g\left( x \right)} \right|dx} \).
Chọn C
Bài 4.39 trang 20 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 4.39 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Thông thường, hàm số sẽ có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm để đơn giản hóa biểu thức.
Lời giải chi tiết:
Để giải bài 4.39, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là: y = (x2 + 1) * sin(x)
Áp dụng quy tắc tích, ta có:
y' = (x2 + 1)' * sin(x) + (x2 + 1) * (sin(x))'
y' = 2x * sin(x) + (x2 + 1) * cos(x)
Vậy, đạo hàm của hàm số y = (x2 + 1) * sin(x) là y' = 2x * sin(x) + (x2 + 1) * cos(x)
Lưu ý quan trọng:
Mở rộng kiến thức:
Ngoài bài 4.39, các em học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức để củng cố kiến thức về đạo hàm. Bên cạnh đó, các em cũng có thể tìm hiểu thêm về ứng dụng của đạo hàm trong các lĩnh vực khác nhau của toán học và khoa học.
Tổng kết:
Bài 4.39 trang 20 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng linh hoạt các quy tắc đạo hàm, các em học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự khác.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và dễ hiểu này sẽ giúp các em học sinh học Toán 12 hiệu quả hơn. Chúc các em học tập tốt!
| Công thức đạo hàm | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x3)' = 3x2 |
| (sin x)' = cos x | (sin 2x)' = 2cos 2x |
| (cos x)' = -sin x | (cos 3x)' = -3sin 3x |