Bài 1.19 trang 16 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.19 trang 16 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một vật được phóng lên trời theo một góc xiên (theta left( {{{45}^ circ } < theta < {{90}^ circ }} right)) so với phương ngang với vận tốc ban đầu là ({v_0}) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc ({45^ circ }) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số (Rleft( theta right) = frac{{v_0^2sqrt 2 }}{{16}}cos theta left( {si
Đề bài
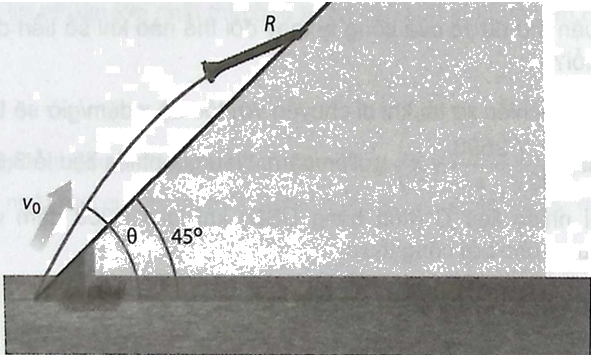
Một vật được phóng lên trời theo một góc xiên \(\theta \left( {{{45}^ \circ } < \theta < {{90}^ \circ }} \right)\) so với phương ngang với vận tốc ban đầu là \({v_0}\) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc \({45^ \circ }\) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số
\(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\)
Góc ném \(\theta \) nào làm cho quãng đường R lớn nhất? Giá trị lớn nhất của R là bao nhiêu?
Phương pháp giải - Xem chi tiết
Xét hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\). Yêu cầu bài toán tương đương tìm giá trị lớn nhất của hàm. Tính đạo hàm, lập bảng biến thiên của hàm số và đưa ra kết luận.
Lời giải chi tiết
Xét hàm số \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos \theta \left( {\sin \theta - \cos \theta } \right)\). Ta cần tìm \(\theta \) để hàm số đạt giá trị lớn nhất.
Ta có \(R\left( \theta \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos \theta \sin \theta - {{\cos }^2}\theta } \right) = \frac{{v_0^2\sqrt 2 }}{{32}}\left( {2\cos \theta \sin \theta - 2{{\cos }^2}\theta } \right)\)
\( = \frac{{v_0^2\sqrt 2 }}{{32}}\left( {\sin 2\theta - \cos 2\theta - 1} \right)\), \(\left( {{{45}^ \circ } < \theta < {{90}^ \circ }} \right)\). Do đó \(R' = \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos 2\theta + \sin 2\theta } \right)\).
Khi đó \(R' = 0 \Leftrightarrow \frac{{v_0^2\sqrt 2 }}{{16}}\left( {\cos 2\theta + \sin 2\theta } \right) = 0 \Leftrightarrow \cos 2\theta + \sin 2\theta = 0 \Leftrightarrow 2\theta = {135^ \circ } \Leftrightarrow \theta = {67,5^ \circ }\)
(do \({45^ \circ } < \theta < {90^ \circ }\)). Mặt khác \(R\left( {{{45}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {45^ \circ }\left( {\sin {{45}^ \circ } - \cos {{45}^ \circ }} \right) = 0\); \(R\left( {{{67,5}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {67,5^ \circ }\left( {\sin {{67,5}^ \circ } - \cos {{67,5}^ \circ }} \right) = \frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}\); \(R\left( {{{90}^ \circ }} \right) = \frac{{v_0^2\sqrt 2 }}{{16}}\cos {90^ \circ }\left( {\sin {{90}^ \circ } - \cos {{90}^ \circ }} \right) = 0\).
Lập bảng biến thiên của hàm số:
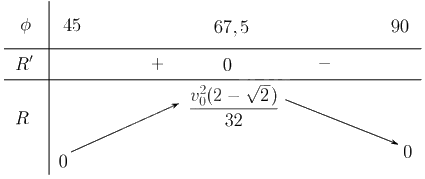
Từ bảng biến thiên suy ra hàm số đạt giá trị lớn nhất tại \(67,5\): \(\mathop {\max }\limits_{\left[ {45;90} \right]} R = R\left( {67,5} \right) = \frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}.\)
Vậy khi góc ném \(\theta = {67,5^ \circ }\) thì quãng đường R là lớn nhất và bằng \(\frac{{v_0^2\left( {2 - \sqrt 2 } \right)}}{{32}}\) feet.
Bài 1.19 trang 16 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Bài tập 1.19 yêu cầu tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể. Các hàm số có thể là các hàm đa thức, hàm phân thức, hàm lượng giác hoặc các hàm số khác.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích và giải chi tiết từng câu hỏi trong bài 1.19 trang 16 Sách bài tập Toán 12 - Kết nối tri thức.
Ta thấy rằng khi x tiến tới 2, biểu thức (x2 - 4) / (x - 2) có dạng 0/0, là một dạng vô định. Ta có thể phân tích tử số thành nhân tử:
x2 - 4 = (x - 2)(x + 2)
Vậy, limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Khi x tiến tới vô cùng, ta có thể chia cả tử và mẫu cho x:
limx→∞ (2x + 1) / (x - 3) = limx→∞ (2 + 1/x) / (1 - 3/x)
Vì limx→∞ 1/x = 0 và limx→∞ 3/x = 0, nên:
limx→∞ (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong việc tính đạo hàm, tích phân và nghiên cứu sự hội tụ của các chuỗi.
Để củng cố kiến thức về giới hạn, các em học sinh có thể tự giải thêm các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 1.19 trang 16 Sách bài tập Toán 12 - Kết nối tri thức và tự tin hơn trong việc học Toán 12.