Bài 3.9 trang 66 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.9 trang 66 sách bài tập Toán 12 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Lợi nhuận của 20 nhà đầu tư quy mô nhỏ ở hai lĩnh vực A và B được cho như sau (lợi nhuận âm được hiểu là lỗ vốn): Hỏi đầu tư vào lĩnh vực nào “rủi ro” hơn?
Đề bài
Lợi nhuận của 20 nhà đầu tư quy mô nhỏ ở hai lĩnh vực A và B được cho như sau (lợi nhuận âm được hiểu là lỗ vốn):
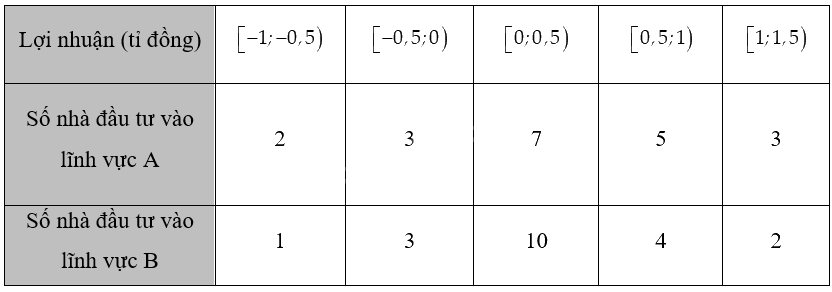
Hỏi đầu tư vào lĩnh vực nào “rủi ro” hơn?
Phương pháp giải - Xem chi tiết
Tính độ lệch của hai mẫu số liệu ghép nhóm, so sánh độ lệch chuẩn của từng lĩnh vực, lĩnh vực có độ lệch chuẩn lớn hơn sẽ có độ rủi ro lớn hơn khi đầu tư.
Lời giải chi tiết
Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
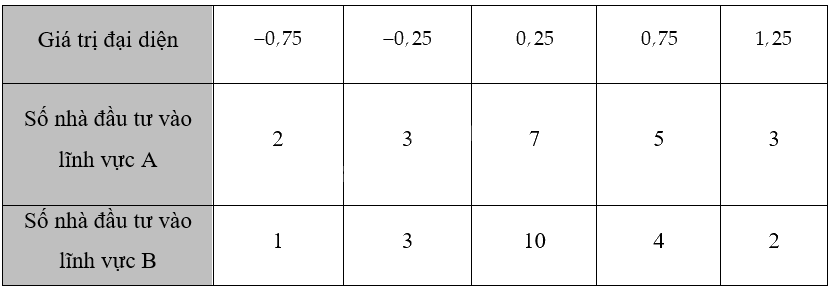
+ Xét mẫu số liệu lợi nhuận của lĩnh vực A
Cỡ mẫu là \(n = 1 + 3 + 10 + 4 + 2 = 20\).
Lợi nhuận trung bình của mỗi nhà đầu tư là
\(\overline x = \frac{1}{{20}}\left[ {2 \cdot \left( { - 0,75} \right) + 3 \cdot \left( { - 0,25} \right) + 7 \cdot 0,25 + 5 \cdot 0,75 + 3 \cdot 1,25} \right] = \frac{7}{{20}} = 0,35\).
Độ lệch chuẩn là
\({s_A} = \sqrt {\frac{1}{{20}}\left[ {2 \cdot {{\left( { - 0,75} \right)}^2} + 3 \cdot {{\left( { - 0,25} \right)}^2} + 7 \cdot {{0,25}^2} + 5 \cdot {{0,75}^2} + 3 \cdot {{1,25}^2}} \right] - {{0,35}^2}} = \frac{{\sqrt {34} }}{{10}} \approx 0,58\).
+ Xét mẫu số liệu lợi nhuận của lĩnh vực B
Cỡ mẫu là \(n = 2 + 3 + 7 + 5 + 3 = 20\).
Lợi nhuận trung bình của mỗi nhà đầu tư là
\(\overline x = \frac{1}{{20}}\left[ {1 \cdot \left( { - 0,75} \right) + 3 \cdot \left( { - 0,25} \right) + 10 \cdot 0,25 + 4 \cdot 0,75 + 2 \cdot 1,25} \right] = \frac{{13}}{{40}} = 0,325\).
Độ lệch chuẩn là
\({s_B} = \sqrt {\frac{1}{{20}}\left[ {1 \cdot {{\left( { - 0,75} \right)}^2} + 3 \cdot {{\left( { - 0,25} \right)}^2} + 10 \cdot {{0,25}^2} + 4 \cdot {{0,75}^2} + 2 \cdot {{1,25}^2}} \right] - {{0,325}^2}} = \frac{{\sqrt 5 }}{{20}} \approx 0,11\).
Suy ra \({s_A} > {s_B}\). Vậy đầu tư vào lĩnh vực A “rủi ro” hơn lĩnh vực B.
Bài 3.9 trang 66 sách bài tập Toán 12 Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Dưới đây là đề bài và lời giải chi tiết bài 3.9 trang 66 sách bài tập Toán 12 Kết nối tri thức:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
f'(x) = 3x2 - 6x
3x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Hàm số f(x) đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số f(x) đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý:
Việc giải bài 3.9 trang 66 sách bài tập Toán 12 Kết nối tri thức không chỉ giúp học sinh nắm vững kiến thức về đạo hàm mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 3.9 trang 66 sách bài tập Toán 12 Kết nối tri thức và áp dụng kiến thức này vào giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!