Bài 2.31 trang 55 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.31 trang 55 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
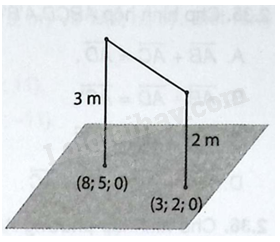
Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của một cột lần lượt là 3 m và 2 m. Xét hệ tọa độ (Oxyz) sao cho mặt phẳng (left( {Oxy} right)) trùng với mặt sân, trục (Oz) hướng thẳng đứng lên trời. Đơn vị trong hệ trục tọa độ được lấy theo mét. a) Biết rằng chân của hai cột có tọa độ lần lượt là (left( {8;5;0} right)) và (left( {3;2;0} right)), hãy tìm tọa độ điểm đầu của mỗi cột. b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. H
Đề bài
Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của một cột lần lượt là 3 m và 2 m.
Xét hệ tọa độ \(Oxyz\) sao cho mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt sân, trục \(Oz\) hướng thẳng đứng lên trời. Đơn vị trong hệ trục tọa độ được lấy theo mét.
a) Biết rằng chân của hai cột có tọa độ lần lượt là \(\left( {8;5;0} \right)\) và \(\left( {3;2;0} \right)\), hãy tìm tọa độ điểm đầu của mỗi cột.
b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. Hỏi sợi dây cần có độ dài tối thiểu là khoảng bao nhiêu mét?
Phương pháp giải - Xem chi tiết
Ý a: Điểm ở đầu cột có cao độ lớn hơn chân cột chiều cao của cột, hoành độ và tung độ thì giống chân cột. Ta suy ra điều này từ mối quan hệ vuông góc.
Ý b: Độ dài tối thiểu của sợi dây có thể có chính là khoảng cách giữa hai đầu chiếc cột.
Sử dụng công thức tính khoảng cách giữa hai điểm.
Lời giải chi tiết
a) Xét đầu chiếc cột có chiều cao 3 m, ta thấy điểm này nằm trên đường vuông góc với mặt phẳng \(\left( {Oxy} \right)\) về hướng theo tia \(Oz\) (hướng lên trên) do đó điểm sẽ có cùng hoành độ và tung độ với điểm ở vị trí chân cột, còn cao độ sẽ lớn hơn 3. Suy ra đầu chiếc cột có chiều cao 3 m có tọa độ là \(\left( {8;5;3} \right)\).
Tương tự xét đầu chiếc cột có chiều cao 2 m, điểm này có tọa độ là \(\left( {3;2;2} \right)\).
b) Độ dài tối thiểu của sợi dây có thể có chính là khoảng cách giữa hai đầu chiếc cột.
Suy ra độ dài tối thiểu của sợi dây là \(\sqrt {{{\left( {8 - 3} \right)}^2} + {{\left( {5 - 2} \right)}^2} + {{\left( {3 - 2} \right)}^2}} = \sqrt {35} \approx 5,92\) (m).
Bài 2.31 trang 55 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 2.31 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Thông thường, hàm số sẽ có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm đã học.
Lời giải chi tiết:
Để giải bài 2.31, ta thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là: f(x) = (x2 + 1) * sin(x)
Ta thực hiện như sau:
Vậy, đạo hàm của hàm số f(x) = (x2 + 1) * sin(x) là f'(x) = 2xsin(x) + (x2 + 1)cos(x)
Lưu ý khi giải bài tập:
Mở rộng kiến thức:
Ngoài bài 2.31, các em học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 - Kết nối tri thức để rèn luyện kỹ năng giải đạo hàm. Bên cạnh đó, các em cũng có thể tìm hiểu thêm về ứng dụng của đạo hàm trong thực tế, chẳng hạn như việc tìm cực trị của hàm số, vẽ đồ thị hàm số, và giải các bài toán tối ưu.
Tổng kết:
Bài 2.31 trang 55 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
| Công thức đạo hàm | Ví dụ |
|---|---|
| (u + v)' = u' + v' | (x2 + 3x)' = 2x + 3 |
| (u - v)' = u' - v' | (x3 - 2x)' = 3x2 - 2 |
| (u * v)' = u' * v + u * v' | (x * sin(x))' = 1 * sin(x) + x * cos(x) |
| (u / v)' = (u' * v - u * v') / v2 | (sin(x) / x)' = (cos(x) * x - sin(x) * 1) / x2 |