Bài 1.39 trang 26 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.39 trang 26, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu có (80000) con. Sau (t) năm số lượng quần thể cá nói trên được xác định bởi (Nleft( t right) = frac{{20left( {4 + 3t} right)}}{{1 + 0,05t}}) (nghìn con). a) Khảo sát sự biến thiên của hàm số (y = Nleft( t right)). b) Số lượng tối đa có thể chứa của quần thể cá là bao nhiêu?
Đề bài
Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu có \(80000\) con. Sau \(t\) năm số lượng quần thể cá nói trên được xác định bởi
\(N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\) (nghìn con).
a) Khảo sát sự biến thiên của hàm số \(y = N\left( t \right)\).
b) Số lượng tối đa có thể chứa của quần thể cá là bao nhiêu?
Phương pháp giải - Xem chi tiết
Ý a: Khảo sát sự biến thiên của hàm số \(y = N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\).
Ý b: Tìm giá trị lớn nhất của hàm số.
Lời giải chi tiết
a) Xét hàm số \(y = N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\).
Tập xác định: \(\left[ {0; + \infty } \right)\).
Sự biến thiên: \(y' = N'\left( t \right) = {\left[ {\frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}} \right]^\prime } = \frac{{56}}{{{{\left( {1 + 0,05t} \right)}^2}}} > 0\) với mọi \(t \ge 0\).
+ Hàm số đồng biến trên khoảng \(\left[ {0; + \infty } \right)\).
+ Hàm số không có cực trị.
+ Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } N\left( t \right) = 1200\)
+ Bảng biến thiên:
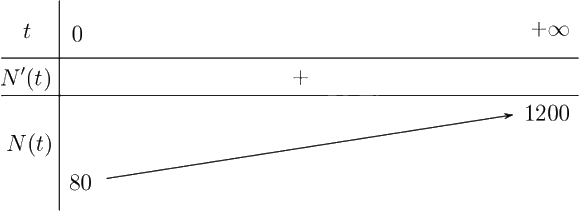
b) Hồ có số lượng cá tối đa khi hàm số \(N\left( t \right) = \frac{{20\left( {4 + 3t} \right)}}{{1 + 0,05t}}\) đạt giá trị lớn nhất.
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số là \(1200\).
Vậy hồ có thể chứa tối đa 1200 nghìn con hay 1200000 con cá.
Bài 1.39 trang 26 sách bài tập Toán 12 Kết nối tri thức là một bài toán ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Để giải bài toán này, học sinh cần nắm vững các kiến thức về đạo hàm của hàm số, điều kiện cần và đủ để hàm số đạt cực trị, và cách sử dụng đạo hàm để khảo sát hàm số.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một vật thể chuyển động theo quy luật s = t^3 - 3t^2 + 5t + 2, trong đó t là thời gian tính bằng giây và s là quãng đường tính bằng mét. Hãy tìm vận tốc và gia tốc của vật tại thời điểm t = 2.)
Để giải bài toán này, ta thực hiện các bước sau:
Vận tốc v(t) là đạo hàm của quãng đường s(t) theo thời gian t: v(t) = s'(t).
Gia tốc a(t) là đạo hàm của vận tốc v(t) theo thời gian t: a(t) = v'(t) = s''(t).
Trong ví dụ trên, s(t) = t^3 - 3t^2 + 5t + 2.
Vậy, v(t) = s'(t) = 3t^2 - 6t + 5.
Và, a(t) = v'(t) = s''(t) = 6t - 6.
v(2) = 3(2)^2 - 6(2) + 5 = 12 - 12 + 5 = 5 (m/s).
a(2) = 6(2) - 6 = 12 - 6 = 6 (m/s^2).
Vậy, vận tốc của vật tại thời điểm t = 2 là 5 m/s và gia tốc của vật tại thời điểm t = 2 là 6 m/s^2.
Các bài tập tương tự bài 1.39 thường yêu cầu học sinh vận dụng đạo hàm để giải quyết các bài toán liên quan đến:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về đạo hàm, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm.
Để học tốt môn Toán 12, các em học sinh nên:
Bài 1.39 trang 26 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!